Technologie GPS

 

avant-propos
Où, sur Terre suis-je?

La réponse à cette question apparemment simple peut parfois être une question de vie et de la mort. Considérez un aviateur en essayant de trouver une destination sûre à la terre, ou l'équipage d'un navire en détresse de demander une assistance ou un randonneur dans les montagnes désorientés par les mauvaises conditions météorologiques. Votre position sur la Terre est d'une importance vitale et peut avoir une immense variété d'implications et applications.

Ils ne doivent pas être aussi dramatique que les circonstances ci-dessus, mais il peut y avoir des situations qui ont également un impact significatif sur notre vie quotidienne. Comment puis-je trouver cette adresse que je cherchais depuis, comment les entreprises peuvent garder une trace de leurs actifs mobiles, comment les gouvernements mettent en œuvre des systèmes de tarification routière, ou quand et où devrait le véhicule de transport en commun déclencher le prochain feu de circulation? Les applications et utilisations des informations de position potentielles sont apparemment sans limites. Notre position sur cette planète bleue a toujours été d'une importance vitale pour les êtres humains et aujourd'hui, notre position exacte est quelque chose que nous pouvons obtenir avec une facilité étonnante.
Parmi les développements technologiques les plus spectaculaires de ces dernières années ont été les immenses progrès dans le domaine de la navigation par satellite ou des systèmes mondiaux de navigation par satellite (GNSS) technologies. Dans une affaire de quelques années, la navigation par satellite a évolué à partir du niveau de la science-fiction à la science fait avec une industrie dynamique et en pleine expansion offrant aux clients dans le monde entier avec la technologie consacrée à la détermination rapide, fiable et facilement disponible de leur position.

En tant que leaders mondiaux dans ce secteur fascinant et en évolution rapide, u-blox AG est une équipe de passionnés de navigation par satellite dédiées avec une tradition d'innovation et de qualité. Dans le cadre de notre engagement envers le service à la clientèle, u-blox est heureux d'être en mesure de vous fournir ce recueil pour vous aider à mener dans le monde remarquable de navigation par satellite.
Le but de ce livre est de fournir une vue d'ensemble de la manière dont fonctionnent les systèmes de navigation par satellite et les applications dans lesquelles ils peuvent être utilisés. Le niveau actuel de développement, ainsi que des changements et de nouvelles avancées seront examinées. Il est écrit pour les utilisateurs qui sont intéressés par la technologie ainsi que des spécialistes impliqués dans les applications de navigation par satellite. Le document est structuré de telle manière que le lecteur puisse diplôme de simples faits à des concepts plus complexes. La théorie de base de la navigation par satellite sera mis en place et complété par d'autres aspects importants. Ce recueil est destiné à servir en outre comme une aide à la compréhension de la technologie qui va spécifiquement en courant navigation par satellite récepteurs, modules et circuits intégrés. De nouveaux développements importants seront traités dans des sections distinctes. L'acquisition d'une compréhension des différents systèmes actuels de coordonnées liés à l'utilisation des équipements GNSS peut être une tâche difficile.

 Par conséquent, un chapitre séparé est consacré à l'introduction de la cartographie.
Nous espérons que ce document sera utile pour vous et que vous serez aussi enthousiaste que nous sommes sur la technologie impliquée dans la détermination de position. Il est en effet un monde immensément fascinant et de l'industrie qui répond à la question «Où diable suis-je?"

introduction
Navigation par satellite est une méthode utilisant un système mondial de navigation par satellite (GNSS) pour déterminer avec précision la position et le temps partout sur la Terre. récepteurs de navigation par satellite sont actuellement utilisés par les particuliers et les entreprises privées pour le positionnement, la localisation, la navigation, l'arpentage et déterminer l'heure exacte à une liste toujours croissante de personnels, les loisirs et les applications commerciales.
L'utilisation d'un système GNSS, les valeurs suivantes peuvent être déterminées avec précision partout sur le globe (Figure 1):
1. Position exacte (longitude, latitude et altitude) coordonnées précises à l'intérieur 20m à env. 1 mm.
2. Heure exacte (Universal Time Coordinated, UTC) précis à 60ns à env. 5ns.

La vitesse et la direction du Voyage (bien sûr) peuvent être dérivées de ces valeurs, qui sont obtenues à partir de satellites en orbite autour de la Terre. Vitesse de Voyage peut également être déterminée directement par des mesures de décalage Doppler. Longitude: 9 ° 24'23.43''Latitude: 46 ° 48'37.20''Altitude: 709.1mTime: 12h33'07 ''

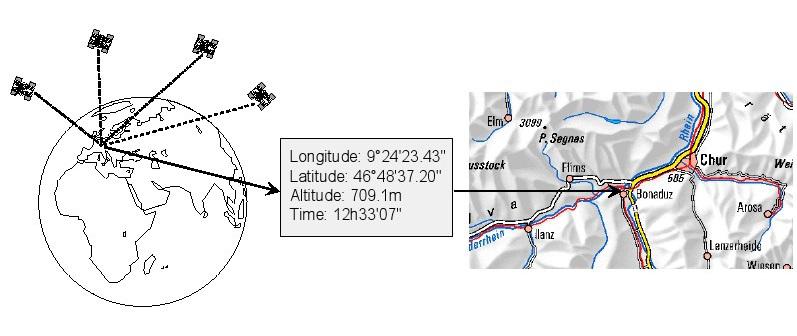
Figure 1: La fonction de base de la navigation par satellite

En 2009, le système de positionnement global (GPS) développé et exploité par le Département américain de la Défense (DoD) a été le système GNSS seulement pleinement opérationnel. L'industrie de navigation par satellite se développe rapidement a vu le jour autour du système GPS, et pour cette raison les termes GPS et de navigation par satellite sont parfois utilisés de manière interchangeable. Ce document mettra l'accent sur le GPS, bien que d'autres systèmes GNSS émergents seront présentés et discutés.
GPS (le nom complet du système est: Système de navigation avec Timing And Ranging Global Positioning System, NAVSTAR-GPS) est destiné à un usage civil et militaire. Les SPS de signaux civils (Service de positionnement standard) peuvent être librement utilisés par le grand public, tandis que le signal militaire PPS (Precise Positioning Service) est disponible uniquement aux organismes gouvernementaux autorisés. Le premier satellite a été placé en orbite le 22 Février 1978, et il est prévu d'avoir un maximum de 32 satellites opérationnels en orbite autour de la Terre à une altitude de 20,180 km sur 6 plans orbitaux différents. Les orbites sont inclinées à 55 ° par rapport à l'équateur, en veillant à ce qu'au moins 4 satellites sont en communication radio avec un point quelconque de la planète. Chaque satellite en orbite autour de la Terre en 12 heures environ et a quatre horloges atomiques à bord.

Au cours du développement du système GPS, un accent particulier a été mis sur les trois aspects suivants:
1. Il avait pour fournir aux utilisateurs la capacité de déterminer la position, la vitesse et le temps, que ce soit en mouvement ou au repos.
2. Il devait avoir un, en tout temps global capacité de positionnement en continu, en 3 dimensions avec un haut degré de précision.
3. Il avait à offrir un potentiel pour un usage civil.

Au cours des cinq ou six prochaines années il y aura probablement 3 systèmes GNSS totalement indépendants disponibles. Les États-Unis continueront à fournir des GPS et de la Russie et l'Union européenne devrait respectivement apporter leur GLONASS et GALILEO systèmes en pleine opération. Tous ces systèmes seront soumis à la modernisation et l'amélioration, ce qui devrait améliorer leur fiabilité et faire de nouveaux services potentiels et les applications disponibles2.

Ce recueil se penchera sur les principes essentiels de la navigation par satellite et aller au-delà de ces dans les applications et technologies spécifiques. GPS recevra une attention particulière en raison de son importance en tant que précurseur et de la norme de l'industrie, et les développements importants tels que Differential-GPS (DGPS), GPS assisté (AGPS) et Interfaces de périphériques seront traités dans des sections distinctes. Ceci est tout dans le but de fournir au lecteur une base solide et la compréhension de ce domaine fascinant et de plus en plus importante.

 

 

 

1 La navigation par satellite en toute simplicité
___________________________________________________________________________________
comprendre, comment la distance de la foudre peut être déterminée simplement?
comprendre, comment la navigation par satellite fonctionne essentiellement?
savent, combien horloges atomiques sont à bord d'un satellite GPS?
savoir, comment déterminer une position sur un plan?
comprendre, pourquoi la navigation par satellite nécessite quatre satellites pour déterminer une position?

___________________________________________________________________________________

1.1 Le principe de signal de mesure du temps de transit

À un moment ou un autre pendant un orage, vous avez presque certainement tenté de travailler sur la façon vous êtes loin d'un coup de foudre. La distance peut être établie assez facilement (Figure 2): distance = le temps l'éclair est perçu (heure de début) jusqu'à ce que le tonnerre se fait entendre (temps d'arrêt) multiplié par la vitesse du son (environ 330 m / s.). La différence entre l'heure de début et d'arrêt est appelée le temps Voyage du signal. Dans ce cas, le signal est des ondes sonores qui se propagent dans l'air.

 

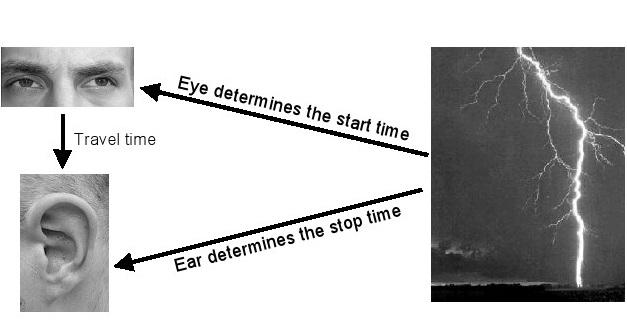
figure 2: Détermination de la distance d'un éclair

fonctions de navigation par satellite par le même principe. On calcule la position en établissant la distance par rapport à la référence des satellites avec une position connue. Dans ce cas, la distance est calculée à partir du temps de Voyage des ondes radio émises par les satellites

1.1.1 Les principes de base de la navigation par satellite

Systèmes de navigation par satellite utilisent tous les mêmes principes de base pour déterminer les coordonnées:
· Satellites avec une position connue transmettent un signal de temps régulier.
· Basé sur le temps Voyage mesurée des ondes radio (signaux électromagnétiques se déplacent dans l'espace à la vitesse de la lumière c = 300'000km / s) la position du récepteur est calculée.

Nous pouvons voir le principe en utilisant plus clairement un modèle simple. Imaginez que nous sommes dans une voiture et devons déterminer notre position sur une rue longue et droite. A la fin de la rue est un émetteur radio d'envoyer une impulsion de signal de temps à chaque seconde. A bord de la voiture que nous menons une horloge, qui est synchronisé avec l'horloge à l'émetteur. En mesurant le temps Voyage écoulé entre l'émetteur et la voiture, nous pouvons calculer notre position sur la rue (Figure 3).

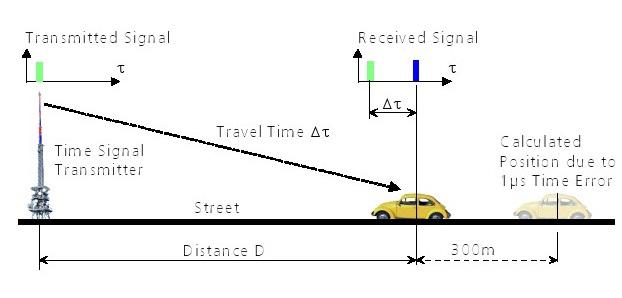
Figure 3: Dans le cas le plus simple la distance est déterminée en mesurant le temps Voyage

La distance D est calculée en multipliant le temps de Voyage par la vitesse de la lumière c.tD

Parce que le temps de l'horloge à bord de notre voiture ne peut pas être exactement synchronisé avec l'horloge à l'émetteur, il peut y avoir un écart entre la distance calculée et réelle parcourue. En navigation cette distance observée en référence à l'horloge locale est appelée pseudo-distance.  d'une microseconde (1μs) génère une pseudo de 300m

Dans notre exemple, un temps de Voyage Dt

Nous pourrions résoudre le problème de la synchronisation d'horloge locale en équipant notre voiture avec une horloge atomique exacte, mais ce serait probablement dépasser notre budget. Une autre solution consiste à utiliser un deuxième émetteur de signal de synchronisation temporelle, pour laquelle la séparation (A) vers le premier émetteur est connue. En mesurant les temps de déplacement, il est possible d'établir exactement la distance (D) en dépit d'une imprécision à bord d'horloge.

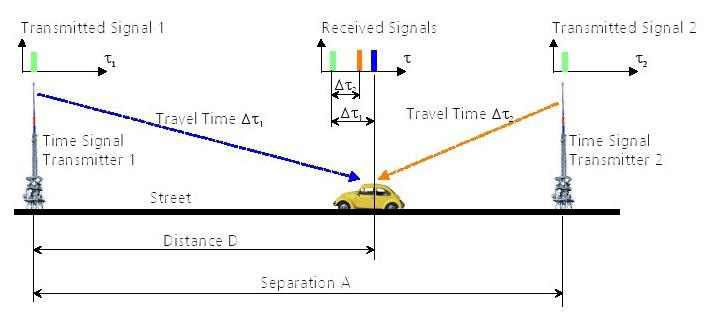
Figure 4: Avec deux émetteurs, il est possible de calculer la position exacte malgré les erreurs de temps.

Comme nous l'avons vu, dans le but de calculer exactement la position et le temps le long d'une ligne (par définition une ligne se développe dans une dimension), nous avons besoin de deux émetteurs de signaux de temps. De cela, nous pouvons tirer la conclusion suivante: Quand une horloge à bord désynchronisé est employé en position de calcul, il est nécessaire que le nombre d'émetteurs de signaux horaires dépasse le nombre de dimensions inconnues par une valeur de un.

Par exemple:
· Sur un plan (agrandissement en deux dimensions), nous avons besoin de trois émetteurs de signaux horaires.
· Dans l'espace en trois dimensions dont nous avons besoin de quatre émetteurs de signaux horaires.

Systèmes de navigation par satellite utilisent des satellites comme émetteurs de signaux horaires. Contactez au moins quatre satellites (figure 5) est nécessaire afin de déterminer les trois coordonnées désirées (Longitude, Latitude, Altitude), ainsi que l'heure exacte. Nous expliquons cela plus en détail dans les sections suivantes.

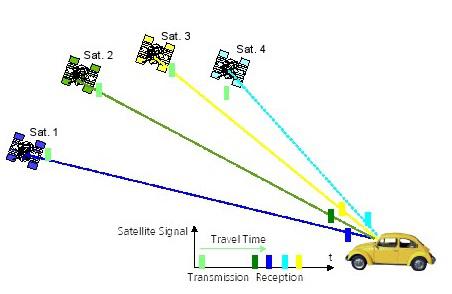
Figure 5: Quatre satellites sont nécessaires pour déterminer la longitude, la latitude, l'altitude et le temps

1.1.2 temps de Voyage de Signal

Systèmes de navigation par satellite utilisent des satellites en orbite au-dessus de la Terre et distribué de telle sorte que d'un point quelconque sur le terrain il y a un contact en ligne de mire au moins 4 satellites.
Chacun de ces satellites est équipé d'horloges atomiques à bord. Les horloges atomiques sont les instruments les plus précis de mesure du temps connus, perdant un maximum d'une seconde tous les 30.000 à 1.000.000 ans. Afin de les rendre encore plus précis, ils sont régulièrement ajustés ou synchronisés à partir de divers points de contrôle sur la Terre. satellites GNSS transmettent leur position exacte et à bord le temps d'horloge sur Terre. Ces signaux sont transmis à la vitesse de la lumière (300000 km / s) et nécessitent donc environ. 67.3ms pour atteindre une position sur la surface de la terre directement au-dessous du satellite. s pour chaque kilomètre supplémentaire de Voyage.mLes signaux nécessitent encore 3.33 Pour établir la position, tout ce qui est nécessaire est un récepteur et une horloge précise. En comparant l'heure d'arrivée du signal de satellite à l'heure de l'horloge à bord du moment où le signal a été transmis, il est possible de déterminer le temps Voyage de signal (figure 6). transmission 0ms25ms50ms75ms0ms25ms50ms75msSignal (heure de début) Satellite clockdisplay etdes: 0msSatellite clockdisplay etdes: réception 67.3msSignal (arrêt du temps) Signal

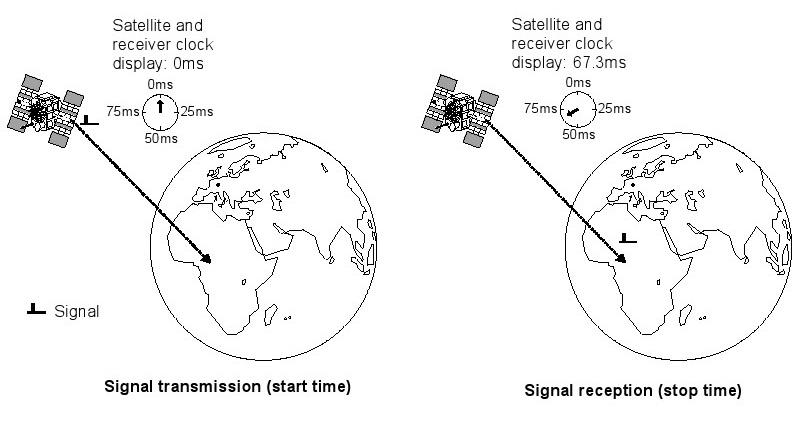
Figure 6: Détermination du temps de Voyage de signal

Comme dans l'exemple de la voiture, la distance D vers le satellite peut être : c • D: latDdéterminée à partir du temps de Voyage de signal connu   GPS-X-02007-D==Dtlumière de la vitesse • ​​Temps traveldistance

1.1.3 Détermination de la position

Imaginez que vous errez à travers un vaste plateau et que vous souhaitez savoir où vous êtes. Deux satellites sont en orbite au-dessus de vous transmettre leurs heures et les positions d'horloge à bord. En utilisant le temps Voyage de signal pour les deux satellites vous pouvez dessiner deux cercles avec le D1 et D2 rayons autour des satellites. Chaque rayon correspond à la distance calculée au satellite. Toutes les positions possibles par rapport aux satellites sont situés sur ces cercles. Si la position au-dessus des satellites est exclue, l'emplacement du récepteur se trouve à l'endroit exact où les deux cercles se croisent au-dessous des satellites (figure 7), par conséquent, deux satellites suffisent à déterminer une position dans le plan X / Y. 

Figure 7: La position du récepteur à l'intersection des deux cercles

Dans le monde réel, la position doit être déterminée dans l'espace tridimensionnel, plutôt que sur un plan. Comme la différence entre un avion et un espace tridimensionnel constitué d'une autre dimension (hauteur Z), un troisième satellite supplémentaire doit être disponible pour déterminer la position réelle. Si la distance par rapport aux trois satellites est connue, toutes les positions possibles sont situés sur la surface de trois sphères dont le rayon correspond à la distance calculée. La position est le point où les trois sphères se croisent (figure 8). Position

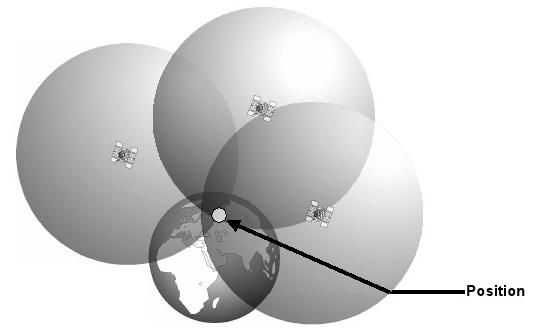
Figure 8: La position est déterminée au point où les trois sphères se croisent

 

 

1.1.4 L'effet et la correction d'erreur de temps

Les conclusions de la section précédente ne sont valables que si l'horloge au niveau du récepteur et les horloges atomiques à bord des satellites sont synchronisés, à savoir, le temps de Voyage de signal peut être déterminé avec précision. Si le temps de Voyage mesurée entre les satellites et un récepteur de navigation earthbound est incorrect de seulement 1μs, une erreur de position de 300m est produite. Comme les horloges à bord de tous les satellites GNSS sont synchronisés, le temps Voyage de signal dans le cas de trois mesures est inexacte par le même montant. Les mathématiques peuvent nous aider dans cette situation.

Lorsque vous effectuez des calculs mathématiques, nous nous souvenons que si N variables sont inconnues, nous avons besoin de N équations indépendantes pour les identifier. Si la mesure du temps est accompagnée d'une erreur inconnue constante (D t) dans l'espace à 3 dimensions, nous aurons quatre variables inconnues:

· longitude (X)
· latitude (Y)
· hauteur (Z)
· Erreur de temps (Dt)

Ces quatre variables nécessitent quatre équations, qui peuvent être dérivées à partir de quatre satellites distincts.
Les systèmes de navigation par satellite sont délibérément construits de telle manière que de tout point de la Terre, au moins 4 satellites sont "visibles" (Figure 9). Ainsi, en dépit d'une imprécision de la part de l'horloge du récepteur et des erreurs de temps en résultant, une position peut être calculée avec une précision d'env. 5 - 10m.

 

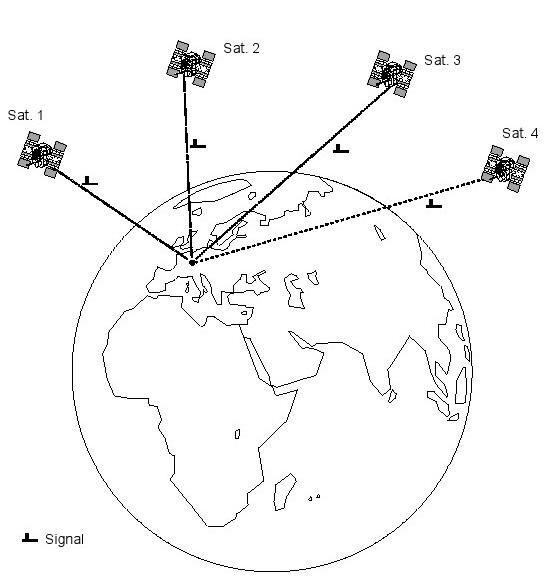
Figure 9: Quatre satellites sont nécessaires pour déterminer une position dans l'espace 3-D.

 

2 systèmes de coordonnées

_____________________________________________________________________________________o savoir ce qu'est un géoïde est
o comprendre pourquoi la Terre est représentée principalement comme un ellipsoïde
o comprendre pourquoi plus de 200 systèmes de référence de carte différents sont utilisés dans le monde entier
o savoir ce que WGS-84 moyens
o comprendre comment il est possible de convertir une donnée dans une autre
o savent ce que les coordonnées cartésiennes et ellipsoïdales sont
o comprendre comment les cartes de pays sont faits
o savent comment les coordonnées du pays sont calculées à partir des coordonnées WGS-84

_____________________________________________________________________________________

2.1 introduction

Un problème important à surmonter lors de l'utilisation d'un système GNSS est le fait qu'il ya un grand nombre de différents systèmes de coordonnées dans le monde entier. Par conséquent, la position mesurée et calculée ne correspond pas toujours à sa position supposée.
Afin de comprendre comment le GNSS fonctionnement des systèmes, il est nécessaire d'examiner quelques-unes des bases de la géodésie: la science qui traite de l'arpentage et de cartographie de la surface de la Terre. Sans cette connaissance de base, il est difficile de comprendre la nécessité apparemment déconcertant de combiner les systèmes appropriés de référence de la carte (points de référence) et les grilles. Parmi ceux-ci, il y a plus de 100 références différentes et environ. 10 grilles différentes à sélectionner. Si une mauvaise combinaison est faite, une position peut être par plusieurs centaines de mètres.

2.2 géoïde

Nous savons que la Terre est ronde depuis Columbus. Mais comment tour est-il vraiment? Décrire la forme de notre planète bleue a toujours été une tâche difficile scientifique. Au cours des siècles plusieurs modèles différents ont été présentés pour représenter une approximation de la vraie forme de la terre le plus fidèlement possible.

Le géoïde représente la vraie forme de la terre; défini comme la surface, où le niveau moyen de la mer est nul. Cette forme est définie par la gravité de la terre, ainsi sa description géométrique est assez complexe. En utilisant le mot grec pour la Terre, cette forme géométrique de cette surface est appelée géoïde (Figure 10).

Parce que la répartition de la masse de la Terre est inégale et, en conséquence, la surface du niveau des océans et des mers ne se trouve pas sur la surface d'une forme géométriquement définissable, des approximations comme ellipsoïdes doivent être utilisés. Qui diffère de la forme réelle de la Terre, un géoïde est un corps théorique, dont la surface de coupe des lignes de champ de gravitation partout à angle droit.

Un géoïde est souvent utilisé comme un niveau de référence pour la mesure de la hauteur. Par exemple, le point de référence en Suisse pour la mesure de la hauteur est le «Repère Pierre du Niton (RPN, 373,600 m) dans le bassin du port de Genève. Cette hauteur provient d'un point à des mesures avec le port de Marseille (hauteur au-dessus du niveau des mers 0.00m moyenne).

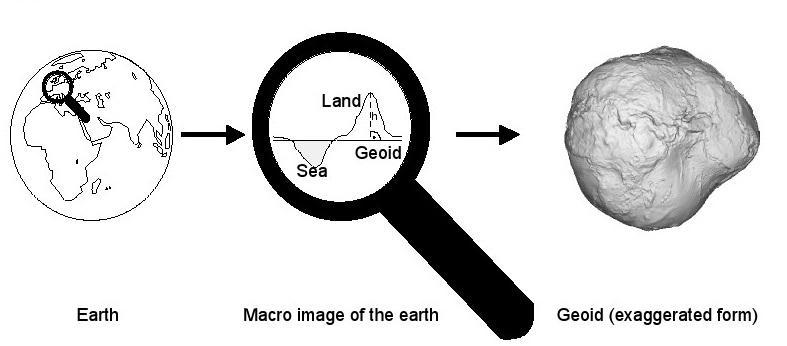
Figure 10: une géoïde est une approximation de la surface de la Terre

2.3 Ellipsoïde et datum

2.3.1 Ellipsoid

Un géoïde est une forme difficile à manipuler lors de la conduite des calculs. Une forme plus simple, plus définissable est donc nécessaire lors de l'exécution des opérations de surveillance quotidienne. Une telle surface de remplacement est connu comme un ellipsoïde. Si la surface d'une ellipse est mis en rotation autour de son axe pôle nord-sud symétrique, un sphéroïde est obtenu sous forme d'un résultat (figure 11).
Un ellipsoïde est défini par deux paramètres:

· Semi axe principal un (sur le plan équatorial)
· Semi axe b (sur l'axe nord-sud pôle)

Le montant dont la forme diffère de la sphère idéale est désignée par aplatissement (f).

 f = (a – b)/a

Figure 11: Production d'un spheroide

 

 

2.3.2 ellipsoïdes de référence locaux sur mesure et référence

2.3.2.1 ellipsoïdes de référence locale

Lorsque vous traitez avec un ellipsoïde, des précautions doivent être prises pour veiller à ce que la perpendiculaire naturelle ne coupe pas verticalement à un point avec l'ellipsoïde, mais plutôt avec le géoïde. ellipsoïdales et perpendiculaires naturels normaux ne coïncident donc pas, ils se distinguent par «déviation verticale» (figure 13), à savoir, les points sur la surface de la Terre ne sont pas correctement projetées. Afin de maintenir cet écart au minimum, chaque pays a développé sa propre ellipsoïde non géocentrique personnalisée en tant que surface de référence pour la réalisation des opérations d'arpentage (figure 12). Les demi axes a et b, ainsi que le point milieu sont choisis de telle manière que le géoïde et rencontres ellipsoïde territoires nationaux aussi précisément que possible.

2.3.2.2 Datum, systèmes de référence de la carte
Les systèmes nationaux ou internationaux de référence de la carte en fonction de certains types de ellipsoïdes sont appelés datums. En fonction de la carte utilisée lors de la navigation avec des récepteurs GNSS, des précautions doivent être prises pour veiller à ce que le système de référence cartographique pertinente a été entré dans le récepteur.
Il y a plus de 120 systèmes de référence de carte disponibles, tels que: CH-1903 pour la Suisse, NAD83 pour l'Amérique du Nord, et WGS-84 en tant que norme mondiale.

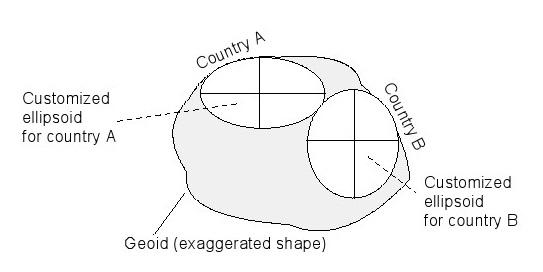
Figure 12: Customized ellipsoïde de référence locale

Un ellipsoïde est bien adapté pour décrire les coordonnées de position d'un point en degrés de longitude et de latitude. Information sur la hauteur est soit basé sur le géoïde ou l'ellipsoïde de référence. La différence entre la hauteur mesurée orthométrique H, à savoir sur la base du géoïde, et la hauteur ellipsoïdale h, sur la base de l'ellipsoïde de référence, est connu comme l'ondulation du géoïde N (Figure 13).

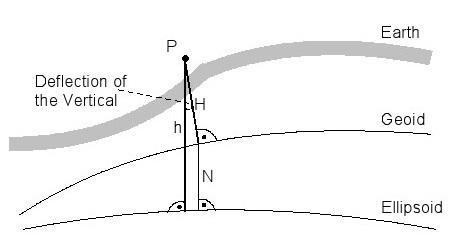
 Figure 13: Différence entre géoïde et ellipsoïde

2.3.3 systèmes nationaux de référence

Les systèmes de référence différents sont utilisés dans toute l'Europe, et chaque système de référence utilisé pour des applications techniques lors de l'arpentage a son propre nom. Ellipsoïdes non géocentriques qui forment la base de ceux-ci sont résumés dans le tableau suivant (tableau 1). Si les mêmes ellipsoïdes sont utilisés, ils se distinguent d'un pays à l'égard de leurs références locales

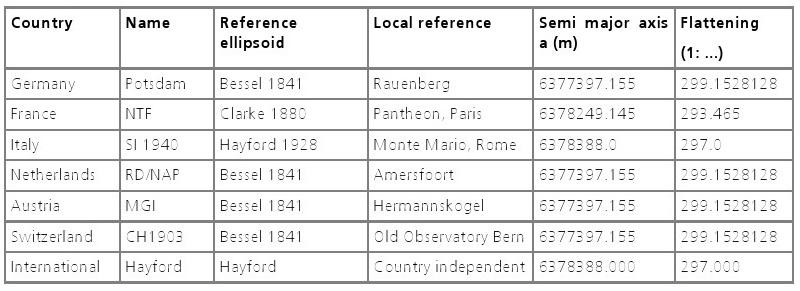
Tableau 1: les systèmes nationaux de référence

 

2.3.4 Référence mondiale ellipsoïde WGS-84

Les détails affichés et les calculs effectués par un récepteur GNSS concernent principalement le WGS-84 (Système géodésique mondial 1984) système de référence. Le système WGS-84 est coordonnée géocentrique positionnée par rapport au centre de la Terre. Un tel système est appelé ECEF (Centré la Terre, la Terre fixe). Le système WGS-84 est une coordonnée tridimensionnelle droitier, système de coordonnées cartésiennes avec son coordonnées initial point au centre de la masse (= géocentrique) d'un ellipsoïde, qui se rapproche de la masse totale de la Terre.

L'axe X positif de l'ellipsoïde (figure 14) se trouve sur le plan équatorial (cette surface imaginaire qui est entouré par l'équateur) et se prolonge à partir du centre de la masse à travers le point où l'équateur et le méridien de Greenwich intersection (le 0 méridien). L'axe des Y se trouve également sur le plan équatorial et est décalé de 90 ° à l'est de l'axe-X. L'axe Z est perpendiculaire au plan X et d'axe Y et se prolonge à travers le pôle nord géographique.

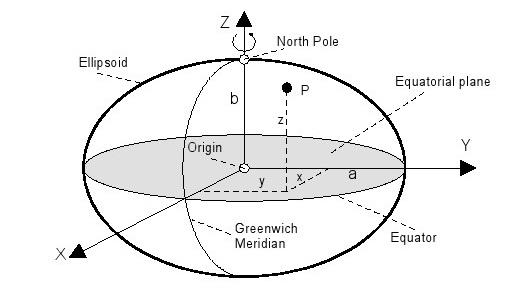
Figure 14: Illustration des coordonnées cartésiennes

Les paramètres de l'ellipsoïde WGS-84 sont résumées dans le tableau 2.

Tableau 2: Le WGS-84 ellipsoïde

coordonnées , h), plutôt que des coordonnées cartésiennes (X, Y,l ,jellipsoïdales ( Z) sont généralement utilisés pour un traitement ultérieur (figure 15). to h à la hauteur lcorresponds la latitude, la longitude et  j ellipsoïdale, à savoir la longueur de la ligne P perpendiculaire à l'ellipsoïde.

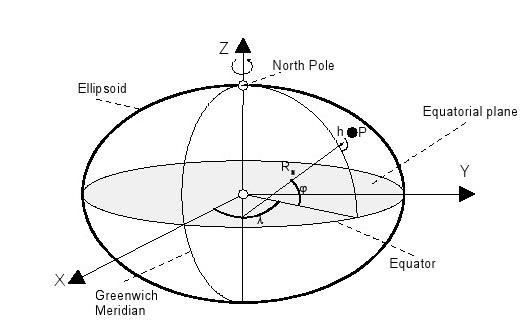
Figure 15: Illustration des coordonnées ellipsoïdales

2.3.5 Transformation du local à travers le monde ellipsoïde de référence

2.3.5.1 datum géodésiques

En règle générale, les systèmes de référence sont généralement locaux plutôt que ellipsoïdes géocentriques. La relation entre un (par exemple CH-1903) local et un système global, géocentrique (par exemple WGS-84) est appelé le système de référence géodésique. Dans le cas où les axes de l'ellipsoïde local et global sont parallèles, ou peuvent être considérés comme étant parallèle pour des applications dans une zone locale, tout ce qui est nécessaire pour la transition de référence sont trois paramètres de décalage, connu comme le décalage du X,Dpoint zéro constantes  Z.DY, D
Trois and un m de facteur d'échelle zjy, jx, jautres angles de rotation  (Figure 16) peut être ajouté afin que la formule de transformation complète contient 7 paramètres. Le système de référence géodésique indique l'emplacement d'un système tridimensionnel de coordonnées cartésiennes locale à l'égard du système mondial.

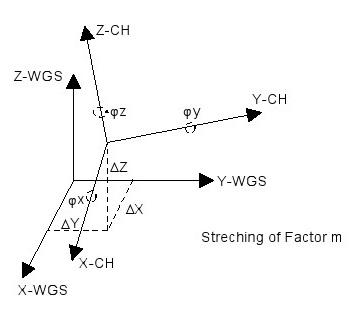
Figure 16: donnée géodésiques

Le tableau suivant (tableau 3) ci-dessous présente des exemples des différents paramètres de référence. D'autres valeurs peuvent être trouvés dans (http://www.geocities.com/mapref/mapref.html).

 

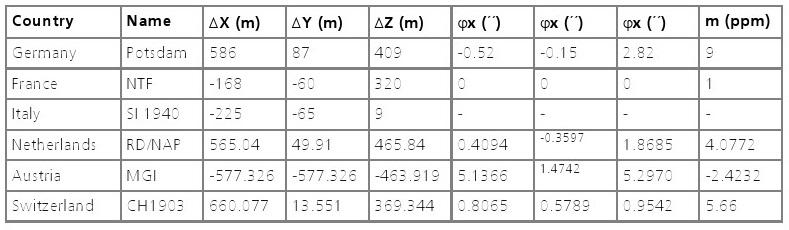
Tableau 3: paramètres de Datum

2.3.5.2 conversion Datum

Convertir une donnée signifie par définition, la conversion d'un système tridimensionnel de coordonnées cartésiennes (par exemple WGS-84) dans un autre (par exemple, CH-1903) au moyen de déplacement en trois dimensions, de rotation et d'extension. Le système de référence géodésique doit être connue, afin d'effectuer la conversion. formules de conversion complètes peuvent être trouvées dans literature (4 B. Hofmann-Wellenhof: GPS in der Praxis, Springer-Verlag, Wien 1994, ISBN 3-211-82609-2 ) spécialiste, ou la conversion peut être effectuée directement via le Internet (Bundesamt für Landestopographie: http://www.swisstopo.ch). Une fois que la conversion a eu lieu, les coordonnées cartésiennes peuvent être transformées en coordonnées ellipsoïdales.

2.3.6 Conversion des systèmes de coordonnées

2.3.6.1 Conversion cartésienne coordonnées ellipsoïdales

coordonnées cartésiennes et ellipsoïdales peuvent être convertis à partir d'une représentation à l'autre. Comme  et h apparaissent sur le côté droit des équations suivantes, cesf équations doivent être évaluées de manière itérative pour une solution précise.

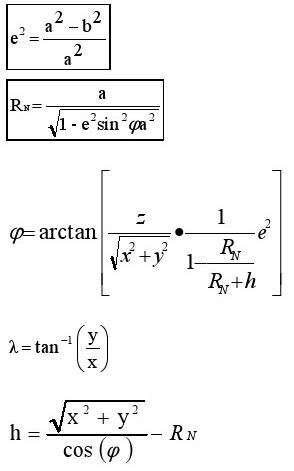
2.3.6.2 Conversion ellipsoïdale en coordonnées cartésiennes

Les coordonnées ellipsoïdales peuvent être converties en coordonnées cartésiennes.

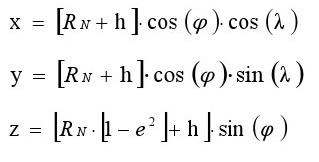
2.4 coordonnées régionales planaires, projection

Habituellement, l'enquête de munitions représente la position d'un point P sur la surface de la terre à travers la latitude les coordonnées  (par rapport à l'ellipsoïde de land longitude  j ellipsoïdales de  référence) et la hauteur (par rapport à l'ellipsoïde ou géoïde).

Étant donné que les calculs du géoïde (par exemple la distance entre deux bâtiments) sur un ellipsoïde sont numériquement maladroit, pratiques techniques d'enquête générale projettent l'ellipsoïde sur un plan. Cela conduit à plat, à angle droit coordonnées X et Y régionaux. La plupart des cartes sont dotées d'une grille, ce qui permet de trouver un point dans l'ouvert facilement. Dans le cas de coordonnées planes régionales il y a des correspondances (projections) de coordonnées ellipsoïdales de l'ellipsoïde de référence de l'enquête dans un plan de calcul. La projection de l'ellipsoïde dans un plan est impossible sans distorsions. Il est cependant possible de choisir la projection de telle sorte que les distorsions soient réduites au minimum. processus de projection habituelles sont cylindriques ou une projection Mercator ou Gauss-Krüger et projection UTM. Si la position d'informations être utilisé en conjonction avec le matériel cartographique, il faut se rappeler que le système de référence et quelle configuration de projection va être utilisé pour la fabrication des cartes.

2.4.1 projection Gauss-Krüger (Transversal Mercator Projection)

La projection de Gauss-Krüger est une transversale conformationnelle Mercator projection tangentielle et est applicable uniquement à une zone ou une région limitée. Un cylindre elliptique est disposé autour de la rotation de l'ellipsoïde de la terre (par exemple Bessel ellipsoïde), dans lequel la surface du cylindre en contact avec l'ellipsoïde dans le méridien central (un méridien important pour la région devant être représentée, par exemple 9 °) sur toute sa longueur et dans les pôles . La position du cylindre par rapport à l'ellipsoïde est transversal, par exemple une rotation de 90 ° (figure 17)). Afin de maintenir les déformations longitudinales et des surfaces à un minimum de 3 ° de larges zones de l'ellipsoïde de rotation sont utilisés. La largeur de la zone est fixée autour du méridien central. méridiens centraux différents sont utilisés en fonction de la région (e. g. 6 °, 9 °, 12 °, 15 °, ....).

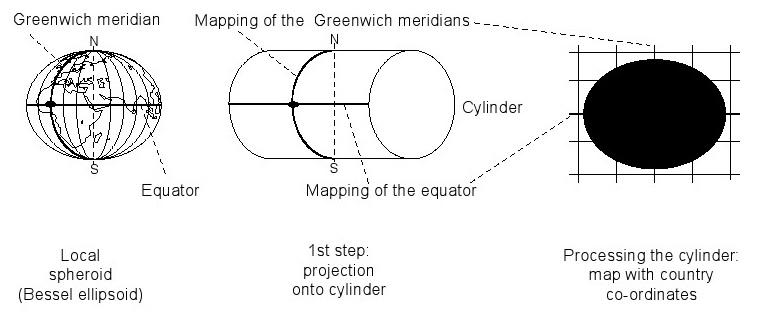
Figure 17: projection Gauss-Krüger

Les valeurs dans la direction nord-sud sont comptés comme la distance de l'équateur. Afin d'éviter les valeurs négatives dans le sens ouest-est la valeur de + 500000m (Offset) est acceptée pour le méridien central. Le numéro du méridien central de degrés est divisé par 3 et placé en face de cette valeur.

Exemple d'une position:
Coordonnées Ellipsoid: N: 46,86154 ° E 9,51280 °
Gauss-Krüger (Central méridienne: 9 °): N-S: 5191454 W-E: 3539097
La position est à une distance de 5191454m de l'équateur et 39097m du méridien central (9 °).

2.4.2 projection UTM

Contrairement à la projection de Gauss-Krüger les UTM (Universal Transversal Mercator) projets de système presque toute la surface de la terre sur 20 = 1200 avions.*60 La projection réelle de l'ellipsoïde de rotation du cylindre transversal est réalisée selon le même procédé que dans la projection de Gauss-Krüger.
Le système UTM est souvent basée sur l'ellipsoïde WGS84. Cependant, il ne définit que la saillie et le système de coordonnées et non l'ellipsoïde de référence et le point de référence géodésique.
Le système UTM divise le monde entier en 6 ° zones longitudinales larges (figure 18). Ceux-ci sont numérotés de 1 à 60 en commençant par 180 ° W, et se terminant avec 180 ° E. Si, pour la zone d'exemple 1 tronçons de 180 ° W à 174 ° W, le méridien central de cette zone 1 est située à 177 ° W, zone 2 tronçons de 174 ° W à 168 °, le méridien central de cette zone 2 est située à 171 ° W, etc.
Les méridiens centraux pour chacune des zones de projection sont de 3 °, 9 °, 15 °, 21 °, 27 °, 33 °, 39 °, 45 °, 51 °, 57 °, 63 °, 69 °, 75 °, 81 °, 87 °, 93 °, 99 °, 105 °, 111 °, 117 °, 123 °, 129 °, 135 °, 141 °, 147 °, 153 °, 159 °, 165 °, 171 °, 177 ° est (E ) et à l'ouest (W) (longitude) (Figure 19).

Dans le sens nord-sud (aux pôles) les zones sont subdivisées, avec une exception dans la ceinture 8 ° de latitude, et sont identifiés par des lettres commençant par C. Seule la zone située entre 80 ° sud à 84 ° au nord est admis. La ligne de 80 ° sud à 72 ° Sud est désignée comme section C, la ligne à partir de 72 ° sud à 64 ° Section D sud, etc. Une exception à cette ceinture est connue sous le nom de latitude X entre 72 ° nord et 84 ° nord. Il est à 12 ° de large.

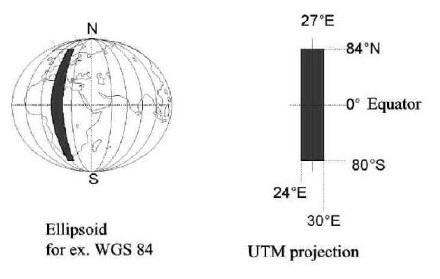
Figure 18: Principe de projeter une zone (de soixante)

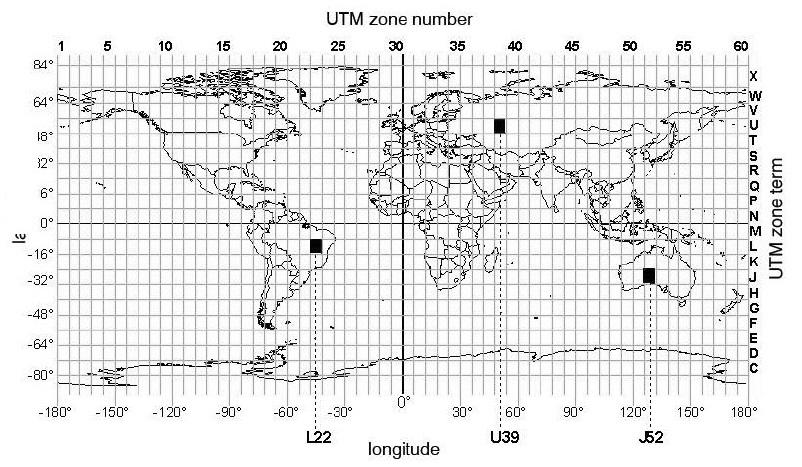
Figure 19: Désignation des zones en utilisant UTM, avec des exemples

Comme cela est le cas avec la projection de Gauss-Krüger, la valeur nord-sud est mesuré en kilomètres que la distance du point de l'équateur. Afin d'éviter les valeurs négatives dans l'hémisphère sud, l'équateur est attribué arbitrairement la valeur de 10,000,000m.
Les valeurs ouest-est sont la distance du point du méridien central, qui (aussi avec la projection de Gauss-Krüger) est donné la valeur de 500,000m.
Un exemple de coordonnées UTM par rapport au WGS 84 serait:
WGS 84:               N ° 46,86074                      E 9,51173 °
UTM: 32 T            5189816 (N-S)                    0539006 (W-E)

2.4.3 système de projection suisse (Conformal Double Projection)

L'ellipsoïde de Bessel est conforme, projeté sur un plan en deux étapes, à savoir l'angle de conservation. Au départ, il y a projection conformationnelle de l'ellipsoïde sur une sphère, la sphère est conforme, projeté sur un plan à l'aide d'une projection cylindrique oblique. Ce processus est appelé double projection (Figure 20). Un point principal est fixé dans le plan sur l'ellipsoïde (ancien observatoire de Berne) dans la projection de l'origine (avec décalage: Yost = 600,000 m et XNord = 200,000 m) du système de coordonnées.

Sur la Suisse de la carte (par exemple l'échelle 1: 25000), il y a deux pièces différentes de coordonner l'information:
· Les coordonnées régionales projetées dans le plan (X et Y km) avec la grille d'accompagnement et
· Les coordonnées géographiques (longitude et latitude en degrés et secondes) liées à la Bessel ellipsoïde

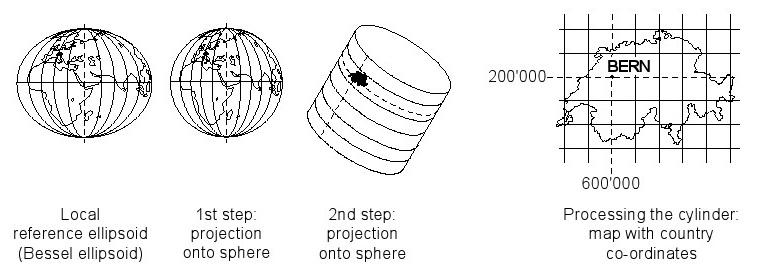
Figure 20: Le principe de la double projection

Le temps de transit de signaux de 4 satellites doit être connue par le temps, les coordonnées de position sont émises. Seulement alors, après le calcul et la conversion considérable, est la position émise en coordonnées d'arpentage suisses (Figure 21).

Figure 21: De par satellite à la position

2.4.4 conversion de coordonnées dans le monde entier

L'Internet offre de nombreuses possibilités pour convertir les coordonnées d'un système à un autre.

2.4.4.1 coordonnées conversion de coordonnées WGS-84 à CH-1903:

 Exemple
(Des systèmes de référence dans la pratique, Urs Marti, Dieter Egger, Office fédéral de topographie) La précision est à moins de 1 mètre!

1. Conversion de latitude et de longitude:

La latitude et la longitude des données WGS-84 doivent être converties en secondes sexagésimaux [''].
Exemple:
1. La latitude (WGS-84) de 46 ° 2'38,87'' fois converti est 165758.87''. Cet entier est décrit comme B: B = 165758.87''.
2. La longitude (WGS-84) de 8 ° 43' 49,79'' fois converti est 31429.79''. Cet entier est décrit comme L: L = 31429.79''.

2. Calcul des entiers auxiliaires:

3. Calcul de l’abscisse  (W – E) : Y

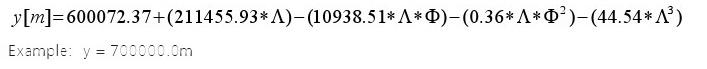
4. Calcul de l’ ordonée (S – N) : X

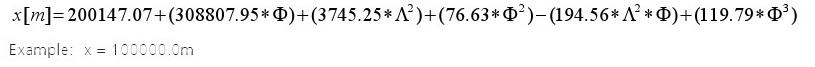
5. Calcul de la hauteur H :

2.5 Géo référencement des cartes raster

2.5.1 Introduction

Géo référencement se réfère à la transformation d'une carte raster (source) dans une carte vectorielle (image). Avec raster cartes l'emplacement de chaque point est donnée par les coordonnées de pixels (X, Y) et peut être stocké dans différents formats de données tels que .JPG, .BMP, .GIF ou .PNG. Ces cartes peuvent être obtenues à partir de photographies satellites ou en scannant des cartes dans un fichier informatique. Avec des cartes vectorielles chaque point est déterminée par les coordonnées géographiques (X ', Y'). La carte raster se transforme en carte vectorielle avec son système de coordonnées géographiques en utilisant une transformation mathématique appropriée (voir Figure 22). Dans cette section, le processus de transformation est expliqué.

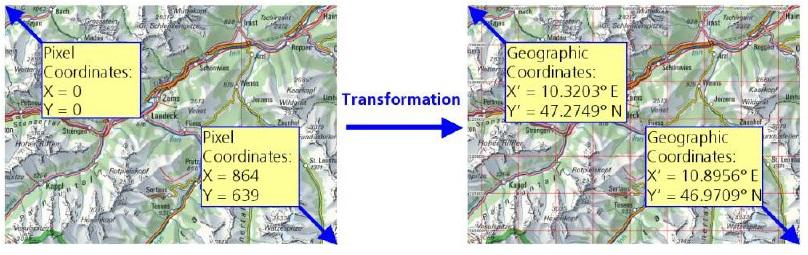
Figure 22: carte Raster avec pixel coordonnées X, Y (à gauche) et le vecteur carte avec des coordonnées géographiques X ', Y' (à droite)

2.5.2 Les bases de la transformation

La transformation d'une carte raster dans une carte vectorielle avec système de coordonnées se fait à travers les règles géométriques de transformation affine. Ceci est également désigné comme une transformation linéaire. La procédure ne convient que pour les petites sections de cartes, couvrant une superficie allant jusqu'à quelques kilomètres. Dans la transformation de coordonnées, les coordonnées de la source du système (X, Y) de coordonnées sont transformées en un autre système (X ', Y').

2.5.3 Détermination de la transformation de coordonnées

Représentation Algébrique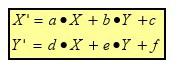

Représentation matricielle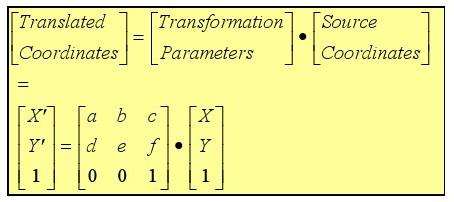    

 

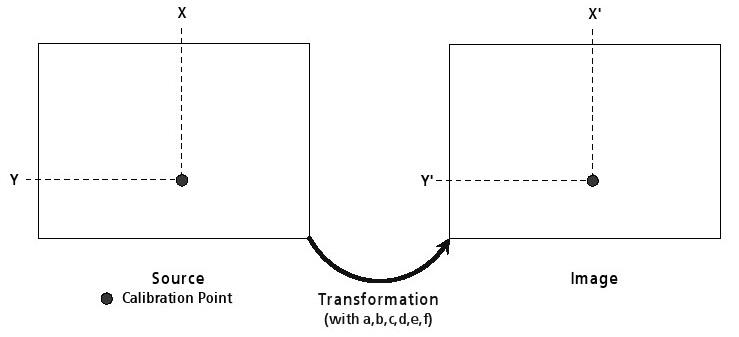
Figure 23: Définition des points de source

2.5.4 Détermination de la transformation de paramètres a, b, c, d, e, f

Les paramètres de transformation 6 (a, b, c, d, e, f) doivent être définies comme 3 paires de coordonnées (points d'étalonnage). Afin de calculer les 6 paramètres, 6 équations à 6 variables inconnues doivent être résolus. La dérivation de la formule afin de déterminer les paramètres de transformation (a, b, c, d, e, f) se produit en 3 étapes.

1. Calibration de l'image:

Trois points d'étalonnage sont sélectionnés qui sont bien réparties sur la carte (voir Figure 24). Les coordonnées de la source (X, Y) et les coordonnées traduites (X ', Y') sont définis pour chacun de ces points d'étalonnage

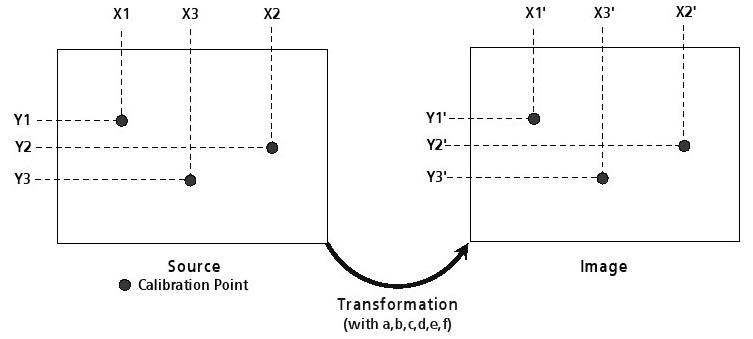
Figure 24: Les points d'étalonnage 3 doivent être bien répartis sur la carte

Calibration Coordonnées:

X1,Y1,X1',Y1'
X2,Y2,X2',Y2' [I]
X3'Y3'X3',Y3'

2. La construction de l'équation de transformation:

Formule [I] peuvent être réorganisés pour tous les 6 des coordonnées transformées

X1'=a•X1+b•Y1+c
Y1'=d•X1+e•Y1+f
X2'=a•X2+b•Y2+c                                                                                                               [II]
Y2'=d•X2+e•Y2+f
X3'=a•X3+b•Y3+c
Y3'=d•X3+e•Y3+f

L'équation [II] est alors représentée sous la forme de la matrice

 [III]
3. La détermination des paramètres de transformation a, b, c, d, e, f:

Les vecteurs de la solution (a, b, c, d, e, f) sont recherchées et peuvent être obtenus en réarrangeant l'équation [III].
[IV]

 

2.5.5 Exemple (raster plan pour WGS84)

La carte suivante (figure 25) doit être géo référencées. Pour la calibration trois points de référence sont utilisés.

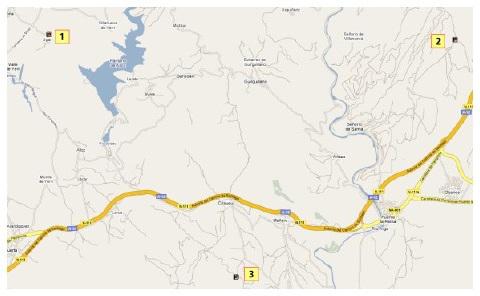
Figure 25: carte Raster avec trois calibration points

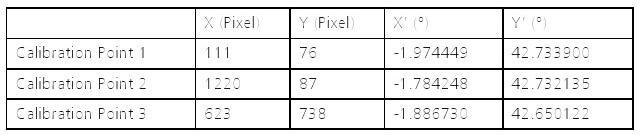
La détermination du paramètre de transformation selon l'équation [IV]

Déterminer les coordonnées d'une position

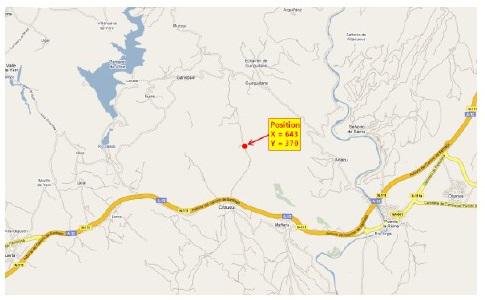
Figure 26: Détermination de la position avec le pixel coordonnées X = 643 et Y = 370

Avec la formule:

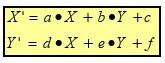
Résultat X' et Y' dans les coordonnées géographiques suivantes:

Longitude X '= - 1.883248 ° et Latitude Y' = 42,69659 °

Figure 27: Vérification des coordonnées géographiques calculées avec Google Earth7

 

3 Fondements de la technologie des satellites

3.1 Les lois de Kepler

Le mouvement des satellites dans l'espace est déterminé par les lois du mouvement planétaire décrit par Johannes Kepler (1571 à 1630). Kepler a observé que le mouvement des corps dans l'espace suivi trois lois mathématiques relativement simples.

3.1.1 La première loi de Kepler

Selon Kepler, les planètes en orbite dans un plan. L'orbite forme une ellipse avec le soleil à l'un des foyers.
Cette loi s’applique également aux satellites (comme des corps en orbite dans l'espace). Les satellites  orbite également dans un plan (figure 28). Leur orbite autour de la Terre forme une ellipse avec la terre à l'un des foyers.

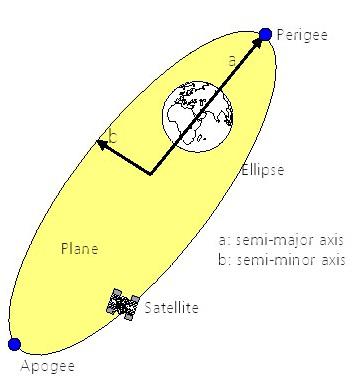
Figure 28: Les satellites se déplacent le long d'un plan

·  L'Apogée exprime le point le plus éloigné d'une orbite elliptique du centre de la Terre. Si l'on soustrait la valeur du rayon de la Terre (env. 6378 km) à partir de cette valeur, on détermine l'altitude maximale du satellite au-dessus de la surface de la Terre.
· Le Périgée est le point de l'ellipse orbitale à la Terre le plus proche. Retranchant le rayon de la Terre détermine l'altitude minimale du satellite au-dessus de la surface de la Terre.

3.1.2 La deuxième loi de Kepler

La deuxième loi stipule que: "Une ligne joignant une planète et le soleil balaie des aires égales pendant des intervalles égaux de temps  " Ceci est également connu comme la loi des aires égales.
Pour les satellites, cela signifie qu'une ligne reliant un satellite et la Terre balaie des aires égales pendant des intervalles de temps égaux. Ainsi, si les temps Tv_1 et Tv_2 sont les mêmes, puis les zones A_1 et A_2 seront également les mêmes (voir Figure 29).

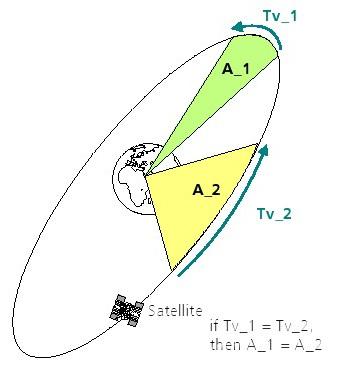
Figure 29: Représentation de la deuxième loi de Kepler

3.1.3 la troisième loi de Kepler

Cette loi stipule que les carrés des périodes orbitales des planètes sont directement proportionnels aux cubes du  demi-grand axe de l'orbite. Cela signifie non seulement que les grands objets ont de plus longues orbites, mais aussi que la vitesse d'une planète en orbite est plus faible que dans une orbite plus petite:  

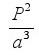 est constante pour toutes les planètes.

P = Période orbitale, a = demi-grand axe de l'ellipse orbitale
De cette loi l'altitude orbitale par satellite (h) (voir Figure 30) au-dessus de la surface de la Terre peut être dérivée:

Re: Rayon de la Terre (6378,137 km)
P: période orbitale du satellite autour de la Terre

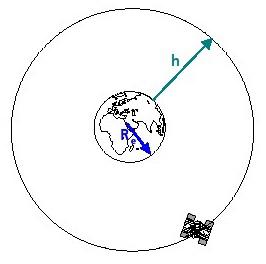
Figure 30: Détermination de l'altitude de l'orbite (h) d'un satellite,

3.2 Les orbite des satellites

L'orbite décrit la position d'un satellite dans l'espace. Les satellites utilisés pour la navigation tournent autour de la Terre sur des orbites circulaires ou elliptiques sans fin. L'orientation spatiale (par exemple d'inclinaison de l'orbite, l'excentricité, la longueur, l'altitude au-dessus du sol) et les paramètres de mouvement (par exemple la période orbitale) ont un impact significatif sur la facilité d'utilisation et les performances de ces satellites (figure 31).

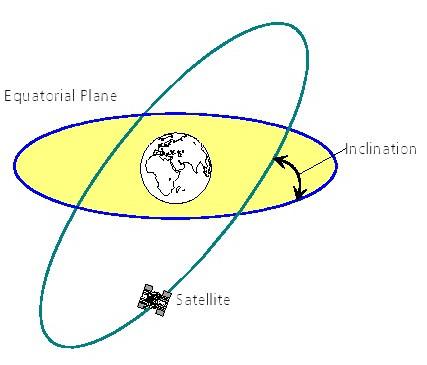
Figure 31: Les orbites des satellites

· L'inclinaison, également désigné sous l'angle d'inclinaison ou l'inclinaison axiale, exprime l'inclinaison de l'orbite circulaire ou elliptique du satellite autour de la Terre par rapport au plan équatorial. Par exemple, avec une inclinaison de 90 ° une orbite passerait directement au-dessus des calottes polaires. Toutes les orbites des satellites qui ne se trouvent pas le long du plan équatorial sont appelés «orbites inclinées».
· L’éphéméride d'un satellite est une description mathématique de son orbite. Les données orbitales de satellite de haute précision est nécessaire pour un récepteur de calculer la position exacte du satellite dans l'espace à un moment donné. Les données orbitales avec précision réduite est appelée un almanach (voir Figure 32). Avec l'aide de l'almanach le récepteur peut calculer quels satellites sont visibles sur l'horizon d’une approximative position et le temps. Chaque satellite transmet sa propre éphéméride ainsi que les Almanachs de tous les satellites existants. Les données actuelles Almanach peut également être consulté sur Internet  ( http://www.navcen.uscg.gov/gps/almanacs.htm).

Figure 32: Almanach

·L'élévation décrit l'angle d'un satellite par rapport au plan horizontal. Si un satellite est directement au-dessus du point d'observation sur le terrain, puis l'élévation est de 90 °. Si le satellite est à l'horizon, puis l'élévation est de 0 °.

·L’Azimuth est l'angle entre un plan de référence et un point. Dans le cas des satellites du plan de référence est le plan de l'horizon sur la base du nord vrai. L’Azimuth est l'angle entre le satellite et le vrai Nord (Nord = 0 °, Est = 90 °, Sud = 180 °, Ouest = 270 °).

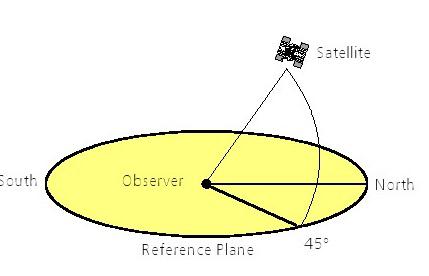
Figure 33: Azimuth

· Excentricité définit le soi-disant "e" numérique Excentricité, qui est la déviation d'une orbite elliptique par satellite (orbite excentrique) à partir d'une orbite géométriquement exacte circulaire. =-Excentricite numérique est définie par l'équation:

où a est le demi-grand axe et b le demi-petit axe de l'orbite elliptique (voir la figure 28). Pour les orbites circulaires complètement la valeur de e = 0, 1 et se rapproche le plus de la longueur (à savoir le demi-grand axe) de l'ellipse est étirée par rapport à l'axe semi-mineur.

3.3 altitude orbitale

L'altitude orbitale donne l'altitude au-dessus de la surface de la Terre d'un point sur une orbite de satellite circulaire ou elliptique. A l'origine, les satellites de communications commerciales ont été préférentiellement mis en équatoriale circulaire (inclinaison 0 °) orbites avec une altitude d'environ 36.000 km au-dessus du sol. Les satellites sur cette orbite tournent autour de la terre en 24 heures (période orbitale: 24 heures), de sorte qu'il n'y a pas de mouvement relatif par rapport à la Terre. Pour cette raison, ces satellites sont aussi appelés géosynchrone (GEO) satellites, avec une orbite dénommée géostationnaires. satellites GEO sont utilisés par les systèmes de satellites de communication tels que les systèmes SBAS tels que WAAS et EGNOS Inmarsat et Thuraya ainsi que (voir la section 7.5.1).
Outre les satellites GEO altitude relativement élevée, ce qui peut fournir une couverture à de vastes zones de la surface de la Terre, d'autres systèmes de satellites (par exemple Iridium, Globalstar, und GPS GALILEO) emploient des satellites avec des altitudes orbitales beaucoup plus faibles. Ces satellites de basse altitude doivent orbite autour de la Terre avec une vitesse accrue afin de fournir la force centrifuge nécessaire pour compenser l'attraction gravitationnelle accrue connu à des altitudes plus basses. Contrairement aux satellites GEO, ces satellites se déplacent par rapport à la Terre et tournent dans soi-disant Orbits satellites non géostationnaires (OSG).

En règle générale, six différentes catégories d'orbites sont classés:
· Orbit terrestre géosynchrone (GEO): orbite géostationnaire à une altitude d'environ 36000 km
· Orbite terrestre moyenne (MEO): orbite inclinée avec une altitude moyenne d'environ 10.000 km
· Terre orbite basse (LEO): orbite basse altitude jusqu'à environ 1'000 km
· Très (Incliné) Elliptique orbite terrestre (HEO)
· Incliné orbite géosynchrone (IGSO)
· Polar Earth Orbit (PEO): LEO orbite au-dessus des calottes polaires

Exemple 1: détermination de l'altitude d'un satellite GEO:
Satellites avec une orbite géostationnaire ont une altitude très précise qui peut être calculée.
La moyenne de la Terre le jour a une durée de 23 heures, 56 minutes, 4.099 secondes = 86164.099 s et représente une rotation géométriquement complète de la Terre de 360 ​​° dans un système avec des étoiles fixes.
De la section 3.1.3 nous savons la formule:

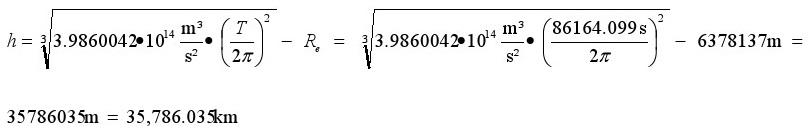
10 par rapport à la position fixe des étoiles

Exemple 2: Détermination de la période de l'orbite d'un satellite GPS.
satellites GPS ont une altitude de niveau moyen de 20,184.5 km de la Terre. La période orbitale moyenne T d'un satellite GPS service est définie par:

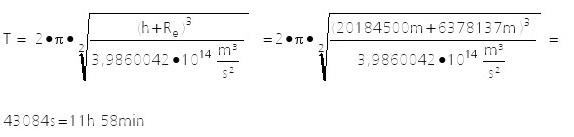
Cela représente une demi-journée sidéral. Depuis la Terre tourne aussi dans ce temps, après deux orbites du satellite GPS va se retrouver sur le même point sur la surface de la Terre.

3.4 Les fréquences radio

La transmission de l'information pour les systèmes de navigation et de télécommunications par satellite a lieu à travers des émissions de radio entre les différentes composantes du système:
· Utilisateur Lien: entre le satellite et l'utilisateur (par exemple terminal utilisateur)
· Feeder lien: entre le satellite et la station centrale sur la Terre (par exemple station au sol, station de contrôle)
· Lien INTERSATELLITES: entre satellites dans l'espace (directement, sans l'aide d'une station au sol)

Transmission est différenciée en fonction de sa direction:
· Upwards (Uplink, ou inversée Link): Transmission de la station de transmission par satellite (station au sol et / ou terminal utilisateur) "up" aux satellites; e.g .: utilisateur en liaison montante, la direction de transmission d'un terminal d'utilisateur mobile
· Downwards (Downlink, Forward Link): Transmission de satellites "vers le bas" à la station de transmission par satellite

Fréquences de transmission par satellite sont affectées et réglementés par la Conférence mondiale des radiocommunications (CMR) de l'Union internationale des télécommunications (UIT). Le tableau 4 montre typique micro-ondes des fréquences de transmissions électromagnétiques utilisées par la communication par satellite et la navigation comme spécifié dans la Recommandation UIT-R V.431-7.

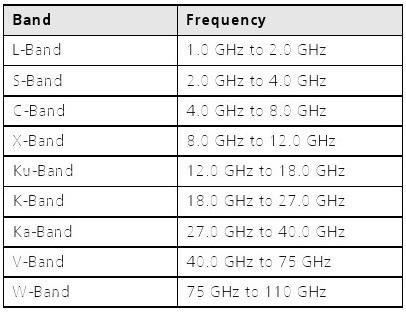
Tableau 4: communication par satellite et de navigation fréquences

3.5 Systèmes de temps
Le temps joue un rôle essentiel dans le positionnement par satellite. GPS distingue cinq différents importants Systèmes temps.

3.5.1 Temps atomique international (TAI)
Le Temps atomique Échelle internationale (Temps Atomique international = TAI) a été introduit afin de produire une échelle universelle "absolue" de temps, ce qui pourrait répondre simultanément aux différentes exigences physiques de diverses applications. Une telle application est le positionnement GPS, pour lesquels cette échelle de temps est très important.
Depuis 1967, le second a été défini par une constante physique atomique. L'élément non radioactif Césium (133Cs) a été choisi comme référence. La fréquence de résonance entre le niveau d'énergie sélectionnées de cet atome a été fixé à 9 192 631 770 Hz. Le temps ainsi défini est devenu une partie du système SI (Système international) des mesures. Le point de temps atomique de départ a été fixé à 1 Janvier, 1958, à 00: 00h.

3.5.2 Temps universel coordonné (UTC)
Temps universel coordonné (UTC) a été introduit afin de fournir une échelle de temps qui est basé sur le temps atomique et adapté au temps réel du monde sur la Terre. UTC a été précédemment appelé Greenwich Mean Time (GMT) ou Zulu-temps ( http://www.bipm.org/en/scientific/tai/time_server.html)
UTC diffère de TAI dans le deuxième chef d'accusation, à savoir UTC = TAI - n, où n est égal secondes entières, qui peut être ajouté à la fin du 31 Décembre et le 30 Juin de chaque année (sauter secondes). Ces secondes intercalaires sont nécessaires pour tenir compte de la tendance au ralentissement général de la Terre et de corriger les horloges qui gardent uniforme, le temps précis.

3.5.3 Temps GPS
Le temps du système GPS général est exprimé en tant que numéro de la semaine et le nombre de secondes écoulées pendant cette semaine. La date de début est le dimanche 6 Janvier 1980, à 0: 00h (UTC). Chaque semaine GPS commence dans la nuit entre le samedi et le dimanche, où l'échelle de temps continue est donnée par l'horloge principale de la station de commande principale. Temps des différences qui se produisent entre le GPS et l'heure UTC sont continuellement calculés et inclus dans les informations de navigation. heure GPS et UTC diffèrent les uns des autres en secondes entières (en 2009, la différence entre l'heure GPS et UTC était de 15 secondes) et une fraction de seconde. Les stations de contrôle GPS garder la différence entre les secondes marques pour l'heure GPS et UTC moins de 1μs. La différence entre le temps GPS et UTC est transmise avec le message de navigation GPS (voir section 4.6) dans le sous-châssis 4.

3.5.4 Temps satellite
En raison des erreurs de fréquence constantes et irrégulières des horloges atomiques à bord des satellites GPS, les temps de satellites individuels dévient de l'horloge du système GPS. La station de contrôle surveille les horloges des satellites, et les différences de temps observées sont communiquées. L'écart de temps doit être pris en considération lors de l'exécution des mesures GPS locales.
~~number=plural

3.5.5 Heure locale
Heure locale se réfère au temps utilisé dans une région ou une zone spécifique. La relation entre l'heure locale et UTC est déterminé par les fuseaux horaires et les règlements pour un gain de temps standard et la lumière du jour.
Le tableau 5 est un exemple d'une heure locale enregistrée le 9 Juillet 2009 à la Suisse.

Tableau 5: systèmes de temps, Janvier 2009 (http://www.leapsecond.com/java/gpsclock.htm)
Pour l'année 2009 les valeurs de temps suivantes sont valides:
· TAI - UTC = + 34sec
· GPS - UTC = + 15sec
· TAI - GPS = + 19sec

4 la technologie GNSS: l'exemple de GPS

---------------------------------------------------------------------------------------------------------------------------------------

o comprendre pourquoi trois segments GPS différents sont nécessaires
o savoir quelle fonction chaque segment a
o savoir comment un satellite GPS est essentiellement construit
o savoir quel type d'information est transmise à la Terre
o comprendre comment un signal satellite est généré
o comprendre comment la navigation par satellite temps de Voyage de signal est déterminé
o comprendre ce que signifie la corrélation
o comprendre pourquoi une période minimum de temps est nécessaire pour le système GPS à venir en ligne
o savent ce que les cadres et les sous-trames sont

----------------------------------------------------------------------------------------------------------------------------------------

4.1 Introduction

Tous les systèmes GNSS fonctionnent sur les mêmes principes de base. Dans les sections suivantes, nous allons explorer les différents segments de la technologie GNSS en regardant spécifiquement au système GPS. GPS est le pionnier et précurseur de la technologie GNSS et est le seul système GNSS pleinement fonctionnel en fonctionnement. GPS et GNSS sont souvent utilisés de façon interchangeable, bien que le GPS se réfère spécifiquement au GPS NAVSTAR, développé par le Département de la Défense des États-Unis et géré par le 50ème Space Wing United States Air Force. Le système GPS est pleinement opérationnel depuis 1993. ( http://en.wikipedia.org/wiki/Global_Positioning_System)

4.2 Description de l'ensemble du système

Le système GPS est composé de trois segments fonctionnels (figure 34):
· Le segment spatial (tous les satellites d'exploitation)
· Le segment de contrôle (toutes les stations terrestres impliqués dans le suivi du système: stations de contrôle maître, stations de contrôle, et les stations de contrôle au sol)
· Le segment utilisateur (tous les utilisateurs civils et militaires)

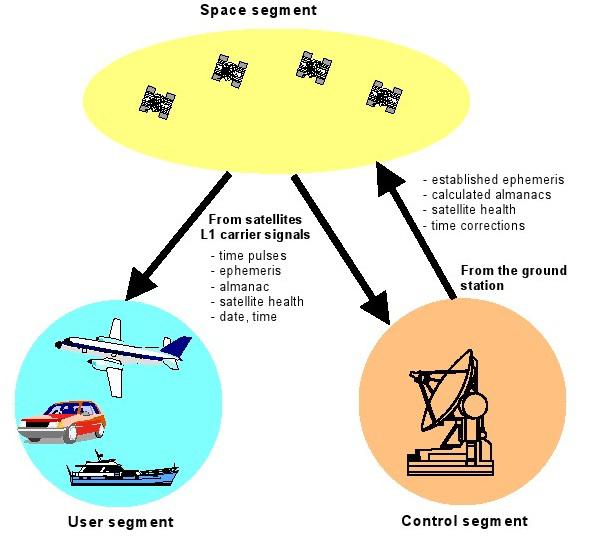
Figure 34: Les trois segments GPS

Comme on peut le voir sur la figure 34, il existe une communication unidirectionnelle entre le segment spatial et du segment utilisateur. Les stations de contrôle au sol ont une communication bidirectionnelle avec les satellites.

4.3 Segment spatial

4.3.1 La distribution et le mouvement satellite

Le segment spatial du système GPS se compose de 32 satellites opérationnels (figure 35) en orbite autour de la Terre sur 6 plans orbitaux différents (quatre à cinq satellites par plan). Ils orbitent à une altitude de 20180 km au-dessus de la surface de la Terre et sont inclinés à 55 ° par rapport à l'équateur. Tout un satellite complète son orbite en environ 12 heures. En raison de la rotation de la Terre, un satellite sera à sa position de départ initiale au-dessus de la surface de la terre (figure 36) après env. 24 heures (23 heures 56 minutes pour être précis).

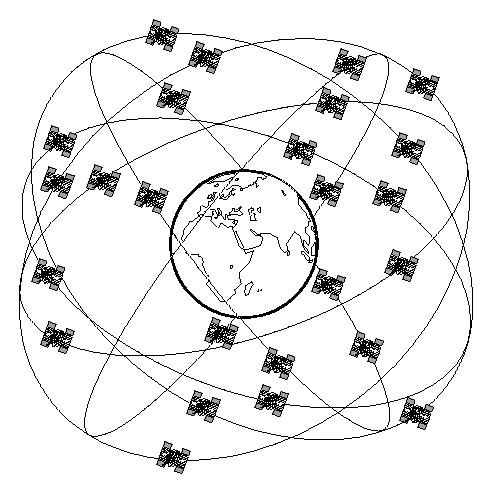
Figure 35: les satellites GPS en orbite autour de la Terre sur 6 plans orbitaux

Les signaux des satellites peuvent être reçus partout à portée effective d'un satellite. La figure 36 montre la portée effective (zone ombrée) d'un satellite situé directement au-dessus du méridien intersection

 

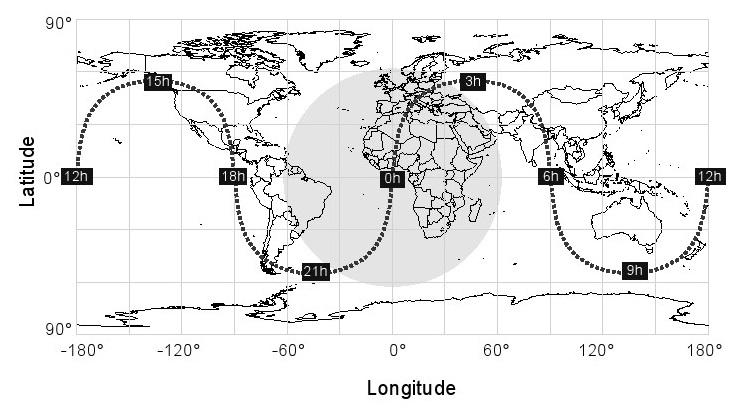
Figure 36: 24 heures suivi d'un satellite GPS avec sa gamme efficace

La distribution des satellites à un moment précis peut être vu dans la figure 37. Elle est due à ce modèle ingénieux de distribution et aux altitudes orbitales élevées que la communication avec au moins 4 satellites est assurée en tout temps partout dans le monde.

 

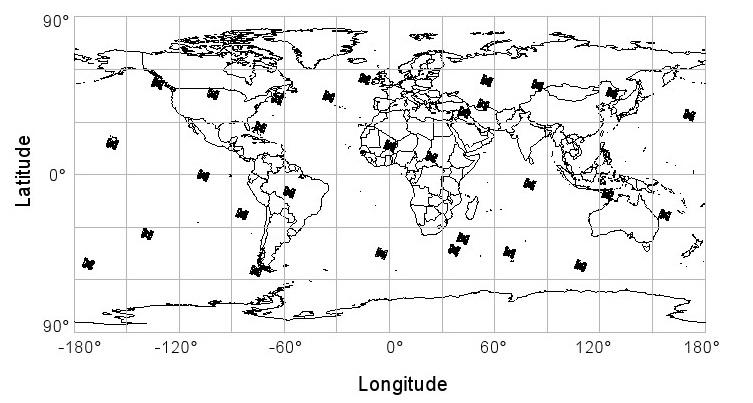
Figure 37: Position des satellites GPS à 12:00 heures UTC le 14 Avril 2001
 

4.3.2 Les satellites GPS
4.3.2.1 construction de satellite
Tous les satellites utilisent à bord des horloges atomiques pour maintenir des signaux synchronisés, qui sont transmis sur la même fréquence (1575,42 MHz). La puissance du signal reçu au minimum sur la Terre est d'environ. -158dBW À -160dBW ( Global Positioning System, la norme de service Système de positionnement, Spécification Signal, 2e édition, 1995, la page 18, http://www.navcen.uscg.gov/pubs/gps/sigspec/gpssps1.pdf). Selon les spécifications, la force maximale est d'environ. -153dBW.

Figure 38: un satellite GPS

4.3.2.2 L'analyse du lien de budget de communication

L'analyse du bilan de liaison (tableau 6) entre un satellite et un utilisateur est adapté pour établir le niveau requis de puissance de transmission par satellite. Selon les spécifications, le montant minimum de la puissance reçue ne doit pas descendre au-dessous -160dBW (-130 dBm). Afin d'assurer ce niveau est maintenu, la puissance de transmission de porteuse L1 par satellite, modulé avec le code C / A, doit être 21.9W. Polarisation décalage et le gain de réception de l'antenne sont fonction de la conception du récepteur. La somme de ces deux paramètres peuvent varier largement. Selon les valeurs de calcul entre +5 dB à -10dB sont typiques.

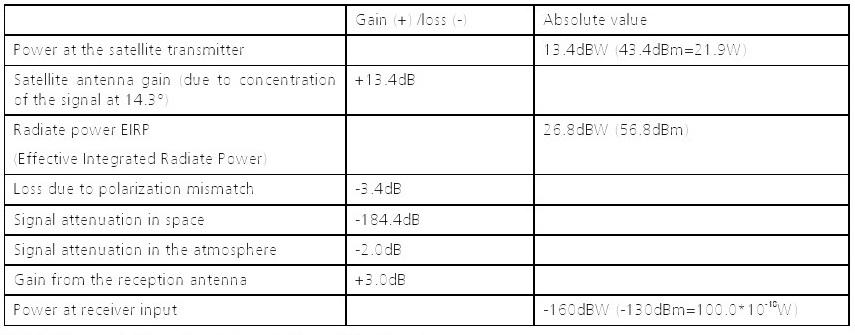
Tableau 6: L1 analyse du budget de liaison de porteuse modulée avec le code C / A

Selon les spécifications, la puissance du signal GPS reçu dans le ciel ouvert est au moins -160dBW (-130 dBm). Le maximum de la densité spectrale de puissance du signal reçu est donnée à titre -190dBm / Hz (figure 39). La densité spectrale de puissance du bruit de fond thermique est d'environ -174dBm / Hz (à une température de 290K). Ainsi, la puissance du signal reçu est au maximum d'environ 16 dB en dessous du niveau de bruit de fond thermique.

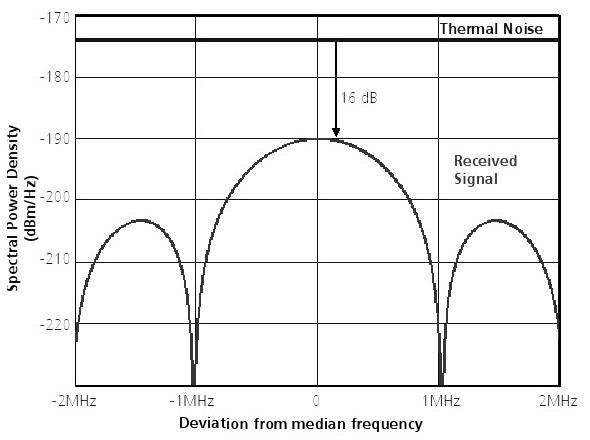
Figure 39: densité spectrale de puissance du signal reçu et le bruit thermique

 

4.3.2.3 Les signaux des satellites

Les informations suivantes (le message de navigation) est transmise par le satellite à une vitesse de 50 bits par seconde [NAVCEN: Spécifications GPS SPS Signal, 2e édition, 1995, http://www.navcen.uscg.gov/pubs/gps/sigspec/gpssps1.pdf]:

--------------------------------------------------------------------------------------------------------------------------------------
· temps de satellite et de signaux de synchronisation
· données orbitales précises (éphémérides)
· Temps information de correction pour déterminer le temps de satellite exacte
· données orbitales approximatives pour tous les satellites (éphémérides)
· signaux de correction pour calculer le signal de temps de transit
· Les données sur l'ionosphère
· Informations sur l'état de fonctionnement (santé) du satellite

----------------------------------------------------------------------------------------------------------------------------------------

Le temps nécessaire pour transmettre toutes ces informations est de 12,5 minutes. En utilisant le message de navigation, le récepteur est capable de déterminer le temps de transmission de chaque signal du satellite et la position exacte du satellite au moment de la transmission.
Chaque satellite GPS transmet une signature unique qui lui est attribué. Cette signature se compose d'un pseudo bruit aléatoire (PRN) Code de 1023 zéros et des uns, diffusé avec une durée de 1ms et continuellement répétée (Figure 40).
011 MS1 ms / 1023

Figure 40: Pseudo bruit aléatoire [Random Noise Pseudo (PRN)]

Le code de signature sert les deux objectifs suivants pour le récepteur:
· Identification: le motif de signature unique identifie le satellite à partir duquel le signal provient.
· Signal mesure du temps de Voyage

 

4.3.3 Génération du signal satellite
4.3.3.1 Schéma simplifié de bloc

Chacun des satellites embarque à sont bord quatre horloges atomiques de haute précision. La fréquence de résonance de l'un de ces horloges génère les impulsions suivantes de temps et les fréquences nécessaires au fonctionnement (figures 13 et 14.)

· L'impulsion de données de 50Hz
· Le C / A (Coarse / Acquisition) code (une diffusion PRN-Code à 1,023 MHz), qui module les données à l'aide d'un ou exclusif opération (EXOR) (Une opération logique sur deux opérandes qui se traduit par une valeur logique vraie si et seulement si exactement l'un des opérandes a une valeur de vrai.  ) diffuser les données sur une bande passante de 2 MHz.
· La fréquence de la porteuse L1 civile (1575.42MHz)

Les données modulées par le code C / A modulent la porteuse L1 à son tour en utilisant Binary-Phase-Shift-Keying (BPSK) (Un procédé de modulation d'une onde porteuse de telle sorte que les données sont traduites en 0/180 ° déphasages de la porteuse).   À chaque changement dans les données modulées il y a un changement de 180 ° de la phase de la porteuse L1.

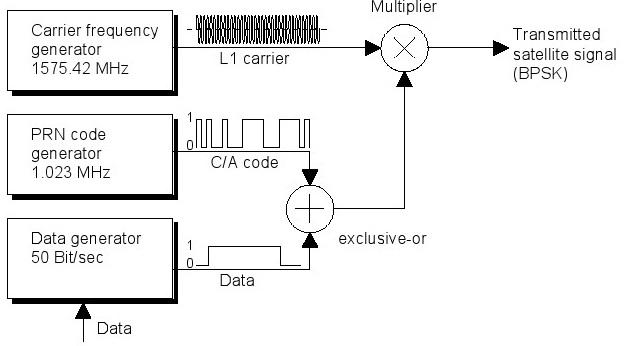
Figure 41: Schéma fonctionnel simplifié par satellite

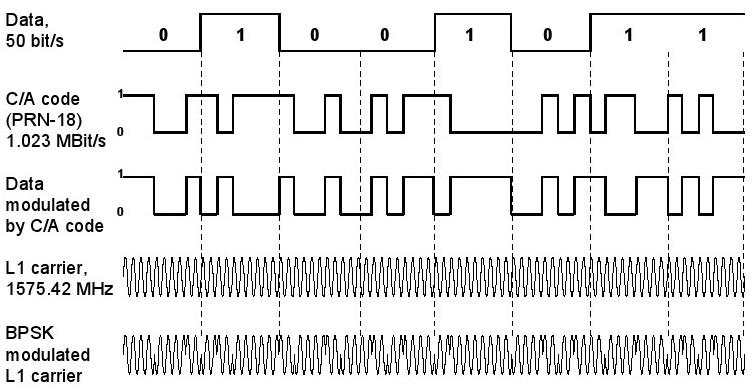
Figure 42: Structure de données d'un signal GPS

4.3.3.2 Détail de schéma de principe

signaux de navigation par satellite sont générés en utilisant un processus connu sous le nom DSSS (Direct Spread Spectrum Sequence) modulation (18). Ceci est une procédure dans laquelle une valeur nominale ou en bande de base (à ne pas confondre avec la puce de bande de base dans le récepteur) la fréquence est délibérément étalé sur une bande passante plus large grâce à la superposition d'un signal de fréquence plus élevée. Le principe de la modulation à spectre étalé a été conçu dans les années 1940 aux États-Unis, par l'actrice écran Hedy Lamarr et pianiste George Anthell (19). Ce processus permet des liaisons radio sécurisées, même dans des environnements difficiles.

Les satellites GPS sont chacun équipés de quatre horloges atomiques extrêmement stables (possédant une stabilité supérieure à 20 · 10exp - 12) (20). La fréquence nominale de la bande de base ou 10.23MHz est produite à partir de la fréquence de résonance d'une de ces horloges embarquées. À son tour, la fréquence porteuse, la fréquence d'impulsion de données et C / A (grossier / acquisition) code sont toutes dérivées de cette fréquence (Figure 43). Etant donné que tous les satellites GPS émettent sur 1575,42 MHz, un procédé connu comme un système CDMA (Code Division Multiple Access) de multiplexage (21) est utilisé.

Le code C / A joue un rôle important dans le multiplexage et la modulation. Il est une séquence constamment répétée de 1023 bits connu comme un bruit aléatoire (PRN) du code pseudo. Ce code est unique pour chaque satellite et sert de signature identifiant. Le code C / A est généré en utilisant un register (22)  décalage à rétroaction. Le générateur a une fréquence de 1,023 MHz et une période de 1023 chips (23), ce qui correspond à 1 ms. C / A code est un Code (24) d'or, qui possède des propriétés de corrélation avantageuses. Ceci a des implications importantes plus tard dans le processus de navigation dans le calcul de la position.

AntennaBPSK modulatorexclusive-ORC / Une période de codegenerator1 = 1ms = 1,023 Chips Transporteur freq.generator1575.42MHzTime impulsion forC / A generator1.023MHz1.023MHzData pulsegenerator50Hz50Hz1575.42MHzDataAtomic clockBaseband Frequency10.23MHz10.23MHzDataprocessing1 Bit = 20ms1.023MHz50Hzx 154: 10: 204'6001.023MHz1575 .42MHz0 / 1C / A codeDataL1 carrierBPSK

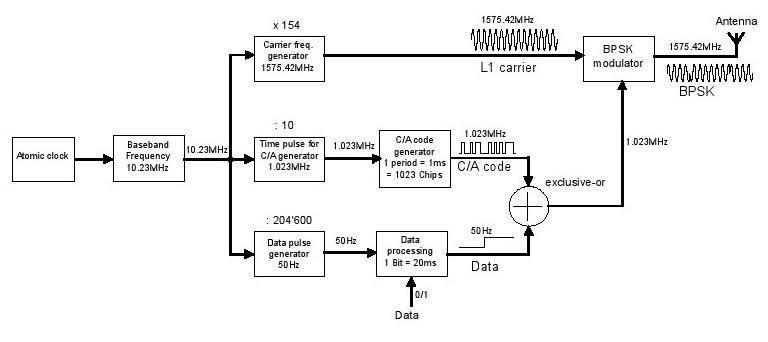
Figure 43: Description détaillée du schéma synoptique d'un satellite GPS

18 Lemme H .: Schnelles Spread-Spectrum-Modem auf einem Chip, Elektronik 1996, H. 15 p. 38 à la p. 45
19 http://www.maxim-ic.com/appnotes.cfm/appnote_number/1890
20 Parkinson B., Système de positionnement global Spilker J, Volume 1, AIAA-Inc.
21 Une forme de multiplexage qui divise un canal radio en utilisant différentes séquences de code pseudo-aléatoire pour chaque utilisateur. CDMA est une forme de signalisation "spectre étalé", puisque le signal de code modulé a une bande passante beaucoup plus élevée que les données communiquées.
22 Un registre à décalage dont le bit d'entrée est une fonction linéaire de son état précédent.
23 temps de transition des bits individuels dans la séquence pseudo-aléatoire.
Code The(24) Un Or isrepresents une séquence binaire qui est généré à partir de deux séquences m de même longueur n. Un ensemble de codes d'or peut être généré par la variation du déphasage de ces deux séquences m. Il est caractéristique pour les codes de Gold que la fonction de corrélation croisée de ces codes suppose que trois valeurs distinctes.

 

 

4.4 segment de commande

Le segment de contrôle du GPS (Operational System Control OCS) se compose d'une station de commande principale située dans l'État du Colorado, cinq stations de contrôle (toutes équipées d'horloges atomiques et distribués dans le monde entier dans le voisinage de l'équateur), et trois stations de contrôle au sol transmettre des informations vers les satellites.
Les tâches les plus importantes du segment de contrôle sont:
· Observer le mouvement des satellites et de calcul des données orbitales (éphémérides)
· Surveillance des horloges des satellites et de prédire leur comportement
· Synchroniser à bord du temps par satellite
· Relayer données orbitales précises reçues de satellites
· Relayer les données orbitales approximatives de tous les satellites (éphémérides)
· Relayer de plus amples informations, y compris la santé par satellite, des erreurs d'horloge, etc.

4.4.1 possibilités de désactivation et la distorsion artificielle du signal (SA)

Le segment de contrôle supervise également la distorsion artificielle des signaux (SA, disponibilité sélective), afin de dégrader la précision de position du système à usage civil. Jusqu'en mai 2000, le DoD américain (les opérateurs de GPS) Précision du système intentionnellement dégradé pour des raisons politiques et stratégiques. Elle consistait soit à moduler les signaux de temps des satellites locales avec un signal d'erreur aléatoire ou falsifier les éphémérides. Au début de mai 2000, le système SA était deactivated25. Avec cette action, la précision de mesure améliorée brusquement d'environ 100 m à 13 m (valeur de 95%) 26 (voir figure 44 et figure 45)

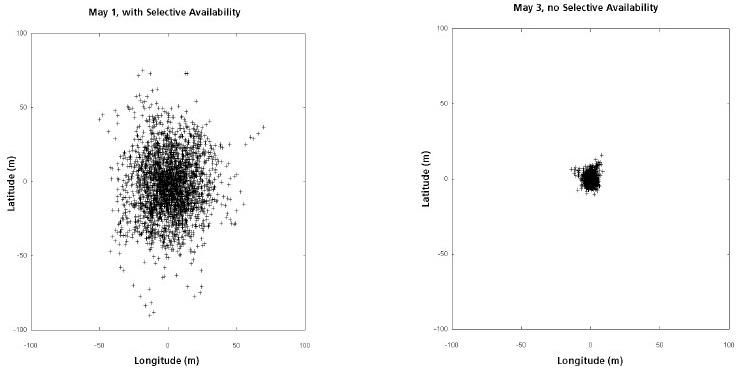
Figure 44: Amélioration de la précision de la position après la désactivation de SA le 2 mai 2000
25 http://www.ngs.noaa.gov/FGCS/info/sans_SA/docs/statement.html
26 http://pnt.gov/public/sa/diagram.shtml

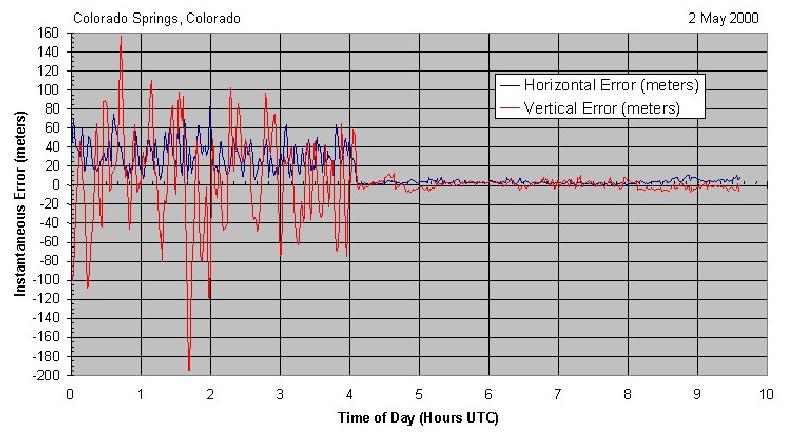
Figure 45: Amélioration de la précision de la position en fonction du temps

Après le 2 mai 2000, la distorsion artificielle (SA) pourrait être régionale ou mondiale réactivée comme nécessaire27. La théorie de cela était de maintenir la possibilité de dégrader ou de limiter la disponibilité du GPS dans des régions spécifiques de crise, tout en assurant la précision du système illimité en dehors de ces zones. Dans la pratique, il n'y avait pas de cas connus de réactivant le système SA.
Le 18 Septembre 2007, le DoD a indiqué que la prochaine génération de satellites GPS (GPS III), des signaux de navigation par satellite ne peuvent plus être artificiellement distorted28, 29. La possibilité technique de distorsion du signal ne sera plus inclus dans cette génération de satellites. Cette décision de la part du gouvernement des États-Unis de ne pas ajouter la capacité de distorsion du signal des satellites GPS III et de ne pas appliquer les mesures de SA existantes devrait garantir la fiabilité du système GPS pour les utilisateurs civils.

4.5 segment de l'utilisateur

Les signaux radio émis par les satellites GPS prennent env. 67 millisecondes pour atteindre un récepteur sur la Terre. Comme les signaux se déplacent à une vitesse constante (la vitesse de la lumière c), leur temps de Voyage détermine la distance exacte entre les satellites et l'utilisateur. Vitesse de la lumière est cependant une fonction du milieu qui sera discuté en détail plus loin.
Quatre signaux différents sont générés dans le récepteur, chacun ayant la même structure que les signaux reçus des 4 satellites. En synchronisant les signaux générés dans le récepteur avec celles des t des quatre satellites sontDsatellites, les temps de signal décalages  mesurés comme une marque de temps (Figure 46). Les t de tous les signaux 4 satellites sontDdécalages temporels mesurés  ensuite utilisés pour déterminer le temps de Voyage de signal exact. Ces décalages temporels multiplié par la vitesse de la lumière sont appelés pseudodistances.
27 http://pnt.gov/public/sa/sa.shtml
28 http://www.defenselink.mil/releases/release.aspx?releaseid=11335
29 http://insidegnss.com/node/200

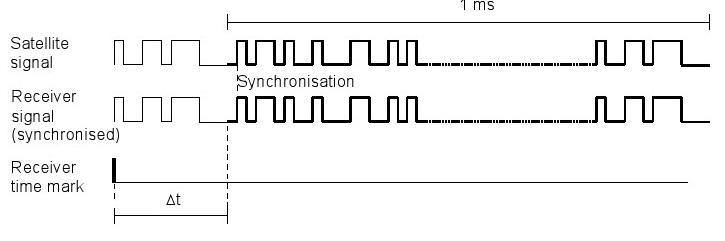
Figure 46: Mesure du temps de Voyage de signal

Afin de déterminer la position d'un utilisateur, une communication radio avec quatre satellites différents est requise. La distance aux satellites est déterminée par le temps Voyage des signaux. Le ,l, longitude jrécepteur calcule alors la latitude de l'utilisateur  altitude h et le temps t à partir des pseudo distances et la position connue des quatre satellites. Exprimée en termes mathématiques, cela signifie que h et t des quatre variables inconnues sont déterminées à partir de la distance et la position de ces quatre satellites connus, même si un niveau assez complexe d'itération est nécessaire, qui sera traitée plus en détail à un stade ultérieur.

Comme mentionné précédemment, tous les satellites GPS émettent sur la même fréquence, mais avec un autre code C / A. Identification de la satellites et le signal de récupération ont lieu au moyen d'une corrélation. Comme le récepteur est capable de reconnaître tous les codes C / A actuellement en cours d'utilisation, par systématiquement décalant et en comparant chaque code connu avec tous les signaux satellites entrants, un match complet finira par se produire (c'est-à-dire le CF de facteur de corrélation est un), et un point de corrélation sera atteint (Figure 47). Le point de corrélation est utilisée pour mesurer le temps de Voyage de signal réel et d'identifier le satellite.

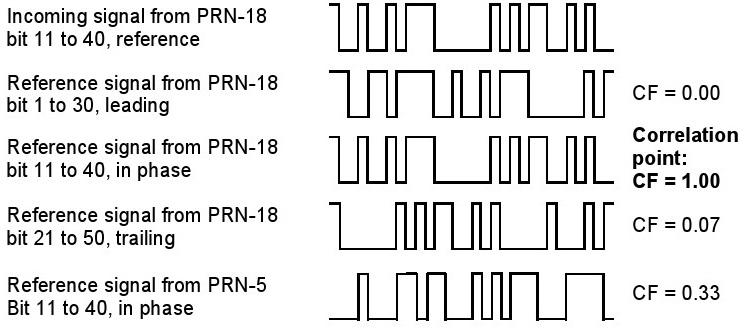
Figure 47: Démonstration du processus de correction à travers 30 bits

La qualité de la corrélation est exprimée ici comme un CF (facteur de corrélation). La gamme des FC de valeur se situe entre moins un et plus un et est seulement plus un lorsque les signaux correspondent complètement (séquence et la phase bit).

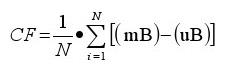
mB: nombre de tous les bits appariés
uB: nombre de tous les bits inégalés
N: nombre de bits observés.

À la suite de l'effet Doppler (satellites et les récepteurs sont en mouvement par rapport à l'autre), les signaux transmis peuvent être 5000 Hz au point de réception.±déplacés jusqu'à  La détermination du temps de Voyage de signal et la récupération de données nécessite donc non seulement une corrélation avec tous les codes possibles à tous les déphasages possibles, mais aussi l'identification de la fréquence correcte porteuse de phase. En outre, la fréquence de référence locale peut aussi avoir un décalage qui ajoute à la plage de fréquences qui doit être recherchée. 1 ppm d'erreur de fréquence de l'oscillateur local correspond à un décalage Doppler 1,575 kHz. 5000 kHz décalage Doppler pour illustration oscillateur local arbitraire.±Figure 48 suppose une certaine décalage au-dessus du  Par déplacement systématique et comparaison de tous les codes (Figure 47) et la fréquence porteuse avec les signaux satellites entrants, il arrive un point qui produit un accord complet (à savoir le facteur de corrélation est un) (Figure 48). Une position de recherche dans le niveau de fréquence de porteuse est connu comme un bac.

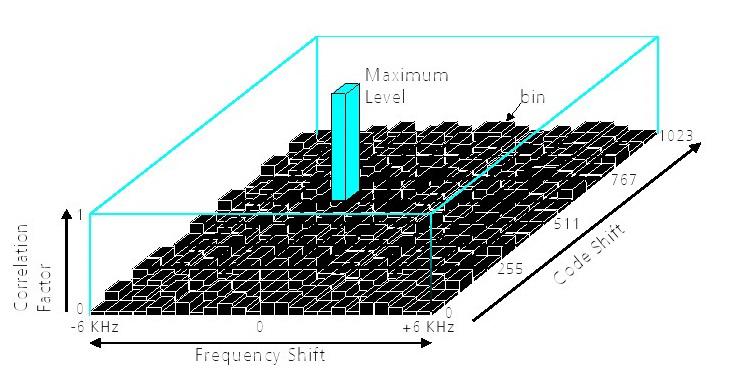
Figure 48: Recherche de la corrélation maximale dans le code et de porteuse domaines de fréquence

La densité spectrale de puissance du signal GPS reçu établit à environ 16 dB en dessous de la densité spectrale de puissance du bruit thermique ou de fond (voir figure 39). La démodulation et désétalement du signal GPS reçu provoque un gain de système G:

Après désétalement, la densité de puissance du signal utile est supérieur à celui du bruit de fond ou signal thermique (figure 49).

Thermal NoiseCorrelated Signal-100Hz-50Hz050Hz100HzDeviation du médian FrequencySpectral densité de puissance (
dBm / Hz) -150-140-160-170-180-190

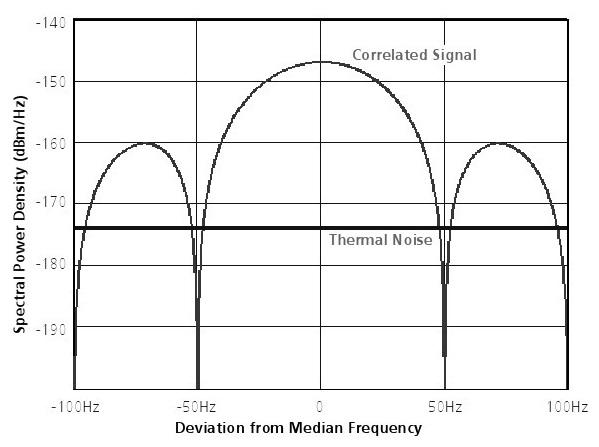
Figure 49: La densité spectrale de puissance du signal corrélé et le bruit du signal thermique

La sensibilité d'un récepteur GPS peut être améliorée en augmentant le temps de corrélation (Dwell Time). Plus un corrélateur reste à un point spécifique dans le domaine de code de fréquence, plus sera la force du signal GPS nécessaire à l'antenne. Lorsque le temps de corrélation est augmentée par un facteur k, il y aura une GR amélioration de la différence entre le signal et le bruit de fond thermique consistant à:

GR = log10 (k)

Doubler le temps Dwell augmente la différence entre le signal et le bruit de fond thermique (la sensibilité du récepteur) par 3dB. En pratique, il ne pose aucun problème pour augmenter le temps de corrélation allant jusqu'à 20 ms. Si la valeur des données transmises est connue, ce temps peut être augmenté encore plus.

4.6 Le message GPS
4.6.1 introduction

Le message30 GPS est un flux continu de données transmises à 50 bits par seconde. Chaque satellite relaie les informations suivantes à la Terre:
· Le temps du système et des valeurs de correction d'horloge
· Ses propres données orbitales de haute précision (éphémérides)
· données orbitales approximatives pour tous les autres satellites (éphémérides)
· L'état du système, etc.

Le message de navigation est nécessaire pour calculer la position actuelle des satellites et de déterminer les temps de déplacement du signal.
Le flux de données est modulé à l'onde porteuse HF de chaque satellite. Les données sont transmises dans des unités regroupées logiquement appelées trames ou pages. Chaque trame est de 1500 bits de long et prend 30 secondes pour transmettre. Les cadres sont divisés en 5 sous-trames. Chaque sous-trame est de 300 bits de long et prend 6 secondes pour transmettre. Afin de transmettre un almanach complet, 25 images différentes sont nécessaires. Le temps de transmission pour l'ensemble de l'almanach est donc de 12,5 minutes. Sauf équipé d'amélioration du GPS (voir le chapitre 7) un récepteur GPS doit avoir recueilli l'almanach complet au moins une fois afin de calculer sa position initiale.

4.6.2 Structure du message de navigation

Un cadre est de 1500 bits de long et prend 30 secondes pour transmettre. Les 1500 bits sont divisés en cinq sous-trames chacun de 300 bits (durée de transmission 6 secondes). Chaque sous-trame est à son tour divisée en 10 mots contenant chacun 30 bits. Chaque sous-trame commence par un mot de télémesure et un mot de transfert (HOW). Un message de navigation complet se compose de 25 images (pages). La structure du message de navigation est illustrée dans un diagramme de la figure 50.

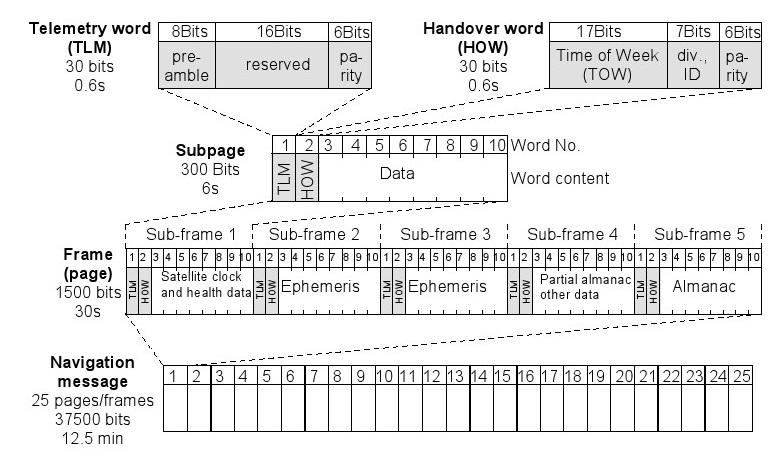
Figure 50: Structure de la totalité du message de navigation

4.6.3 Les informations contenues dans les sous-trames

Un cadre est divisé en cinq sous-trames, chaque sous-trame transmettant des informations différentes.
· Chassis 1 contient les valeurs de temps du satellite émetteur, y compris les paramètres de correction de temps de transit du signal et l'heure de l'horloge à bord, ainsi que des informations sur la santé par satellite et d'une estimation de la précision de la position du satellite. Sous-trame 1 transmet également la soi-disant numéro de semaine 10 bits (une plage de valeurs de 0 à 1023 peuvent être représentés par 10 bits). temps GPS a commencé le dimanche 6 Janvier 1980, à 00:00:00 heures. Tous les 1024 semaines, le numéro de la semaine redémarre à 0. Cet événement est appelé une «semaine roulement».
· Les sous-trames 2 et 3 contiennent les données d'éphéméride du satellite émetteur. Ces données fournissent des informations extrêmement précises sur l'orbite du satellite.
· Chassis 4 contient les données d'almanach sur le nombre de satellites 25 à 32 (N.B. chaque sous-trame peut transmettre des données d'un seul satellite), la différence entre le GPS et l'heure UTC (secondes intercalaires ou UTC offset) et les informations concernant les erreurs de mesure provoquées par l'ionosphère.
· Chassis 5 contient les données d'almanach sur le nombre de satellites 1 à 24 (N.B. chaque sous-trame peut transmettre des données d'un seul satellite). Les 25 pages sont transmis ensemble avec les informations sur la santé des numéros de 1 à 24 satellites.

4.6.4 TLM et HOW ,SLT et COMMENT

Le premier mot de chaque image, le mot de télémesure (TLM), contient une séquence de préambule 8 bits de longueur (10001011) utilisés à des fins de synchronisation, suivis de 16 bits réservés pour les utilisateurs autorisés. Comme avec tous les mots, les 6 derniers bits du mot de télémétrie sont des bits de parité.
Le mot de Handover (HOW) suit immédiatement le mot de télémétrie dans chaque sous-trame. Le mot de Handover est de 17 bits de longueur (une gamme de valeurs 0-131071 peut être représenté en utilisant 17 bits) et contient dans sa structure l'heure de début de la prochaine sous-trame, qui est transmis au fil du temps de la semaine (TOW). Le nombre de TOW commence par la valeur 0 au début de la semaine GPS (période de transition du samedi 23:59:59 heures au dimanche 00:00:00 heures) et est augmentée d'une valeur de 1 toutes les 6 secondes. Comme il existe 604,800 secondes dans une semaine, le compteur va de 0 à 100 799, avant de revenir à 0. Un marqueur est introduit dans le flux de données toutes les 6 secondes et le faire transmis, afin de permettre la synchronisation avec le code P. Bit Nos. 20 à 22, sont utilisés dans le mot de transfert afin d'identifier le sous-châssis juste transmise.

4.6.5 Subdivision des 25 pages

Un message de navigation complet nécessite 25 pages et dure 12,5 minutes. Une page ou un cadre est divisé en cinq sous-trames. Dans le cas des sous-trames 1 à 3, le contenu d'information est la même pour toutes les 25 pages. Cela signifie qu'un récepteur a la complète des valeurs d'horloge et de données d'éphémérides du satellite de transmission toutes les 30 secondes.
La seule différence dans le cas de sous-trames 4 et 5 est de savoir comment les informations transmises sont organisées.
· Dans le cas des sous-châssis 4, pages 2, 3, 4, 5, 7, 8, 9 et 10 relayer les données d'almanach sur le nombre de satellites 25 à 32. Dans chaque cas, les données d'almanach pour un seul satellite est transféré par page. Page 18 transmet les valeurs de correction pour les mesures à la suite de la scintillation ionosphérique, ainsi que la différence entre l'UTC et le temps GPS. Page 25 contient des informations sur la configuration de l'ensemble des 32 satellites (à savoir le bloc d'affiliation) et la santé des numéros de satellite 25 à 32.
· Dans le cas de sous-trame 5, pages 1 à 24 relais les données d'almanach sur le nombre de satellites 1 à 24. Dans chaque cas, les données d'almanach pour un seul satellite est transféré par page. Page 25 transfère les informations sur la santé des numéros de satellite 1 à 24, et le temps d'almanach d'origine.

4.6.6 Comparaison entre les éphémérides et les données d'almanach

En utilisant les deux éphémérides et almanachs données, les orbites des satellites et donc les coordonnées pertinentes d'un satellite spécifique peut être déterminée à un point défini dans le temps. La différence entre les valeurs transmises réside principalement dans la précision des chiffres. Dans le tableau suivant (Tableau 7), une comparaison est faite entre les deux séries de chiffres.

Tableau 7: Comparaison entre les éphémérides et les données d'almanach

L'orbite d'un satellite suit une ellipse. Pour une explication des termes utilisés dans le tableau 7, voir Figure 51

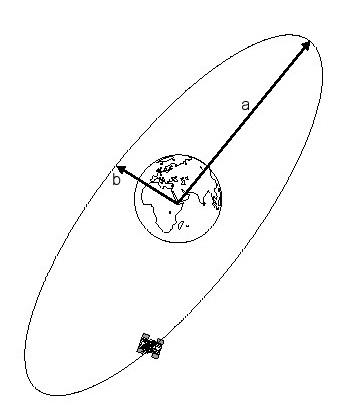
Figure 51: Conditions de éphémérides
  

4.7 modernisation GPS

4.7.1 Nouvelle procédure de modulation, BOC et MBOC

4.7.1.1 BPSK (1) –modulation

Pour que tous les satellites émettent sur la même fréquence, les signaux GPS sont dispersés (modulée) avec un code spécial. Pour les signaux civils du système de positionnement standard (SPS) de ce code est constitué d'un pseudo aléatoire Noise code (PRN) de 1023 zéros ou ceux et est connu sous le nom / A-Code C. Le code, avec une période de 1 milliseconde, a un débit des éléments 1.023Mbit / s. Il est continuellement répété et en raison de sa structure unique permet au récepteur d'identifier à partir de laquelle le signal satellite est originaire.
L'étalement (ou la modulation) du signal de données est réalisée avec un (EXOR) ou-exclusif fonctionnement (figure 52). Le résultat est appelé Binary Phase Shift Keying (BPSK (1)). Le signal de fréquence de consigne ou de la bande de base est générée par l'une des horloges atomiques et tous les signaux satellites sont dérivés de ce produit. La fréquence nominale ou en bande de base est alors étalée ou modulée par le / A Code C à 1 • 1.023Mbit / s.

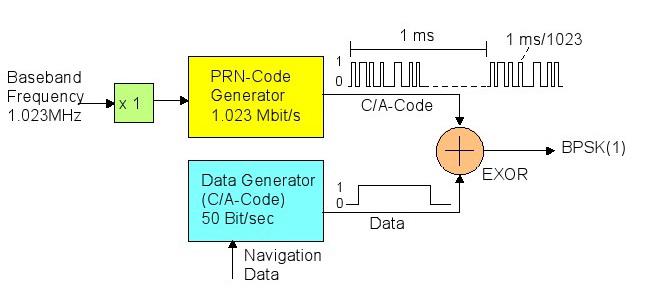
Figure 52: En ce BPSK du signal de données de navigation est tout d'abord transmis par un code

La densité spectrale de puissance (PSD) du BPSK (1) des signaux est illustré sur la figure 53.
Densité spectrale de puissance (dBm / Hz)
Déviation de fréquence médiane

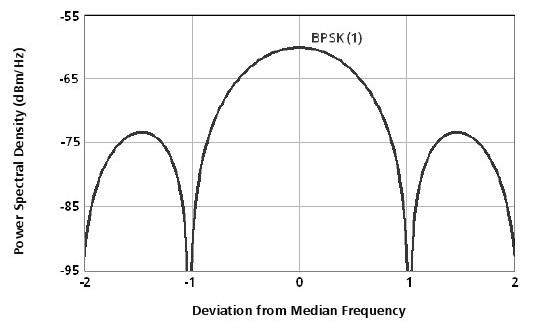
Figure 53: densité spectrale de puissance de BPSK (1) des signaux (intensité du signal normalisé à 1 W par signal)

4.7.1.2 Introduction de la BOC-modulation

Dans la modulation de base de avenir L'eau Une pour GPS et les systèmes GALILEO européenne sera un nouveau procédé de modulation appelé Binary Offset Code Modulation (BOC). Avec BOC le signal BPSK subit une nouvelle modulation31. La fréquence de modulation est toujours un multiple de la fréquence de bande de base de 1,023 MHz. Les propriétés de cette modulation sont communiquées d'une manière spécifique. Par exemple BOC (10,5) signifie que la fréquence de modulation est un facteur de 10 fois la fréquence nominale ou Baseband (10 • 1,023 MHz) et le débit des éléments du code C / A est de 5 fois la base (5 • 1,023Mbit / s) (figure 54).

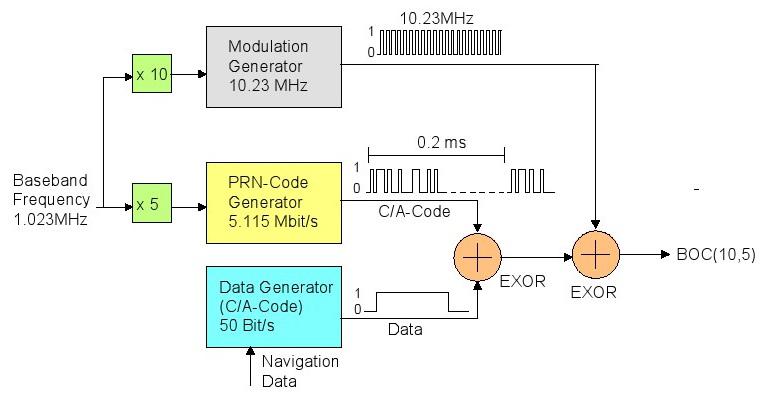
Figure 54: Bloc schématique d'un BOC (10,5) modulateur

Avec le signal BOC est mieux répartie sur la largeur de bande et l'influence de la réflexion du signal opposées (multipath) à la réception du signal de navigation est réduite par rapport à BPSK. BPSK (1) et BOC (1,1) ont un impact minimal sur l'autre quand il est utilisé en même temps parce que leurs maxima de densité spectrale de puissance sont séparés (figure 55).
31 Journal de l'Institut de la navigation, 2002, Vol.48, n ° 4, pp 227-246, Auteur: John W. Betz Densité spectrale de puissance (dBm / Hz)
Déviation de fréquence médiane

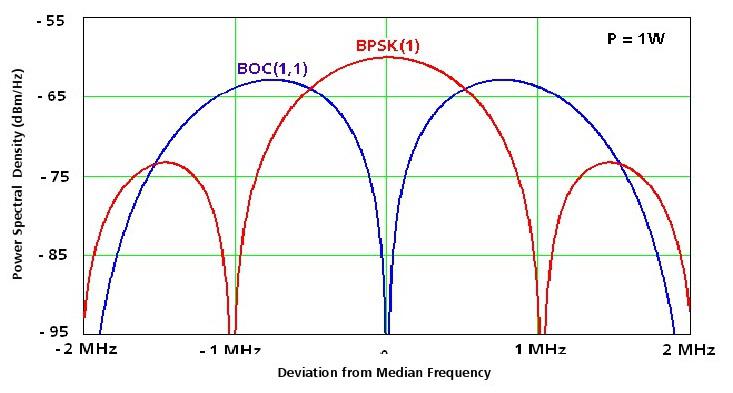
Figure 55: Avec BPSK (1) et BOC (1,1) les maxima de signal sont séparés (force du signal normalisé à 1 W par signal)

4.7.1.3 MBOC modulation (multiplexé BOC, MBOC (6,1,1 / 11)

Le 26 Juillet 2007, les Etats-Unis et l'UE ont convenu que le GPS et GALILEO utilisent le même type de modulation. La nouvelle modulation, connu sous le nom MBOC (6,1,1 / 11), sera utilisé avec le nouveau signal GPS L1C (L1 civile) et pour le GALILEO signaux L1 OS (L1 Open Service, parfois appelé E1). MBOC modulation est une extension de la modulation BOC, et combine deux modulateurs de BOC et ajoute les signaux avec une pondération différente (figure 56)

Figure 56: MBOC (6,1,1 / 11) modulateurs pour L1C et L1 OS

En combinant deux signaux BOC, plus de performance est disponible à des fréquences plus élevées (figure 57). En tant que performances de suivi des résultats sont améliorée et le récepteur est moins sensible au bruit, les interférences et les multi trajets. Afin de tirer profit de toutes les propriétés, la bande passante du récepteur doit être d'environ 20 MHz (BPSK (1) env. 2 MHz).
Densité spectrale de puissance (dBm / Hz)
Déviation de fréquence médiane

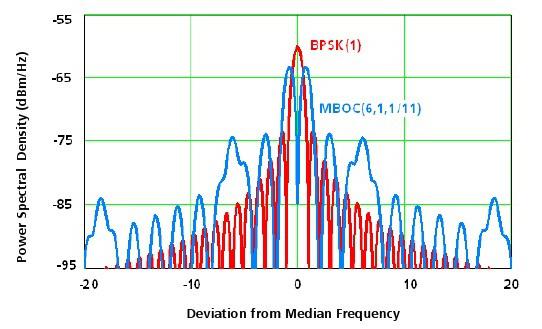
Figure 57: densité spectrale de puissance de MBOC (6,1,1 / 11) par rapport à BPSK (1) (P = 1W par signal)

 

4.7.2 modernisation GPS
Etant donné que l'activation du système GPS en 1978, tous les satellites émettent les trois signaux suivants à la Terre:
· Sur la L1-Fréquence (1575.42MHz): un signal civil (SPS-Service avec le C / A-Signal, BPSK (1)) et un signal militaire (PPS-service avec la P (Y) -Signal, BPSK (10 ))
· Sur la L2-Fréquence (1227.60MHz): un deuxième P (Y) -Signal pour des applications militaires.

Le DoD américain a prévu des améliorations progressives à la structure du signal GPS (Figure 59). Pour des applications civiles de l'introduction d'une deuxième et une troisième fréquence est très importante; lorsque plusieurs fréquences peuvent être utilisées pour établir la position, puis l'influence de l'ionosphère sur le temps de Voyage de signal peut être compensé ou même éliminé. Cette compensation est possible car le c32 de la vitesse de transmission de la ionosphère est dépendante de la fréquence. Outre les deux nouveaux signaux, la modernisation de GPS fournira une augmentation de l'intensité du signal pour les utilisateurs civils ainsi que des capacités supplémentaires pour des applications militaires.
Les opérateurs de GPS ont le plan de temps suivant pour modernization33 GPS:
À la fin de 2009, huit nouveaux satellites du type IIR-M (Bloc 2, reconstitution et militaires) mis en orbite. IIR-M satellites émettent des signaux supplémentaires tels que:
· Un nouveau signal civil à une fréquence de 1227,60 MHz, le signal que l'on appelle L2C.
· D'autres signaux militaires à 1575,42 MHz et 1227,60 MHz: les signaux M. Ces signaux M emploient BOC (10,5) modulation.
Après la fin de 2009, 24 satellites du type GPS IIF (Bloc 2, Suivez-ON) sera mis en orbite (Figure 58, left34). La caractéristique la plus importante de ces satellites est:
· satellites IIF transmettent un nouveau signal civil à une fréquence de 1176,45 MHz (L5 Fréquence). Ce signal est plus robuste que les signaux civils précédents et peut être utilisé dans l'aviation au cours des approches critiques.

Figure 58: GPS IIF satellite (à gauche) und GPS III satellite (à droite)

Après 2013, une nouvelle génération de satellite est prévu. Cette nouvelle série aura la désignation GPS III (Bloc 3) (Figure 58, right35). La caractéristique la plus importante de ces satellites sont:
· Augmentation de la puissance du signal des M signaux (= M+) par le déploiement d'antennes à faisceau concentré.

32 Environ 300.000.000 m / s
33 Ray Clore, GPS Constellation Update, TimeNav'07 Systèmes de Navigation Etat, Genève 2007
34 http://www.boeing.com/defense-space/space/gps/index.html
35 http://www.aero.org/publications/crosslink/summer2002/07.html

• · Amélioration du rapport C / Une structure de signal de la fréquence L1-civil. Le nouveau signal sera désigné L1C.
  · Transmission d'un signal d'intégrité
  · Recherche et sauvetage capacités
  · Non intégré capacité technique pour produire la dégradation artificielle (disponibilité sélective, SA)

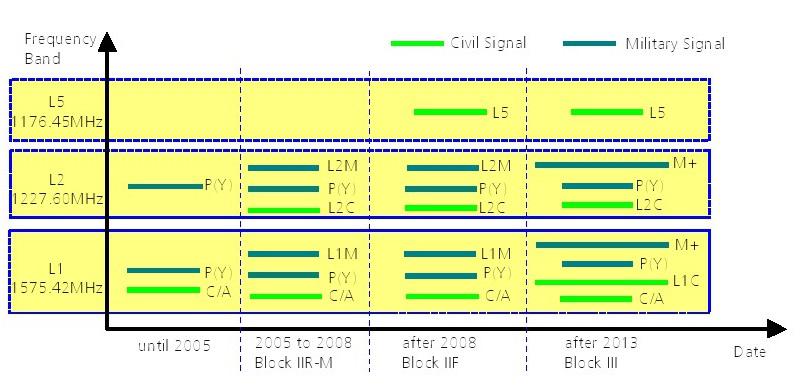
Figure 59: Avec la modernisation du nombre de fréquences GPS disponibles sera augmentée

Les stations au sol GPS seront également renouvelées. L'ensemble de la révision du système devrait être complet et opérationnel en 2021. Les nouveaux signaux seront alors entièrement à la disposition des utilisateurs.

5 GLONASS, GALILEO et Beidou / Compass

Veux-tu . . .
o savoir, comment fonctionne le système de navigation GLONASS russe
o comprendre, pourquoi GLONASS sera construit
o savoir, quel système Europe sera l'activation
o comprendre, pourquoi GALILEO fournira différents services
o savoir, ce que SAR peut signifier pour les marins
o savoir, comment les nouvelles fonctions de BOC processus de modulation
o savoir, sur le système prévu par la République populaire de Chine
puis ce chapitre est pour vous!

5.1 introduction

Le 28 Décembre 2005, le premier satellite GALILEO a été mis en orbite. En 2014 il y aura probablement trois systèmes GNSS indépendants disponibles: GPS, GLONASS et GALILEO. GPS sera également modernisé dans un proche avenir et deviendra donc plus fiable (voir section 4.7). Ce chapitre donne un aperçu du système GLONASS existant, le futur système européen GALILEO et le système GNSS prévu par la République populaire de Chine: Beidou / Compass.

5.2 GLONASS: le système russe

GLONASS est une abréviation pour un système GNSS actuellement exploité par le Ministère de la Défense russe. Le GLONASS de désignation signifie Système mondial de navigation par satellite. Le programme a été lancé par l'ex-Union soviétique, et est aujourd'hui sous la juridiction de la Communauté des États indépendants (CEI). Les trois premiers tests-satellites ont été lancés en orbite le 12 Octobre 1982.

Les faits les plus importants du système GLONASS sont les suivants:
· 24 satellites prévus (21 standards + 3 satellites de réserve). Ce nombre n'a jamais été atteint. Au début de 2008, on comptait 14 satellites en service (Figure 6036). La relativement courte durée de vie des satellites individuels de 3 à 4 ans entravé l'achèvement du système.

Figure 60: Statut du GLONASS en Juillet 2009

36 http://www.glonass-ianc.rsa.ru/pls/htmldb/f?p=202:20:2776707736388438778... GPS-X-02007-D

• · 3 niveaux orbitaux (figure 6137) avec un angle de 64,8 ° par rapport à l'équateur (ce qui est l'angle le plus élevé de tous les systèmes GNSS et permet une meilleure réception dans les régions polaires)

Figure 61: Les trois orbitales de GLONASS

· altitude orbitale de 19.100 km et période orbitale de 11h15.8min
· Chaque satellite GLONASS transmet deux codes (C / A et P-code) sur deux fréquences. Chaque satellite transmet le même code, mais à des fréquences différentes dans les environs de 1602MHz (L1 Band) et 1246 MHz (L2 Band). Les fréquences peuvent être déterminées par la formule suivante (k est le canal de fréquence du satellite considéré):
o Fréquence en L1 Band: f1 = 1602 MHz + k • (9/16) MHz
o Fréquence en L2 Band: f2 = 1246 MHz + k • (7/16) MHz

5.2.1 Achèvement du GLONASS

Le système GLONASS nécessite 24 satellites fonctionnels pour un déploiement complet. Le CIS a l'intention d'avoir son système pleinement opérationnel. A intervalles réguliers, un Proton-K DM-2 lance trois satellites GLONASS-M (satellites Uragan) en orbite (Figure 6238). La série M ont une durée de vie de 7-8 ans et de transmettre 2 signaux civils.

37 Sergey Revnivykh, 46-ème Réunion CGSIC, Fort Worth, TX, USA, 26 Septembre, 2006
38 http://www.nasa.gov/multimedia/imagegallery/index.html

Figure 62: GLONASS-M satellite et le lancement d'une fusée Proton-K-DM2

Après 2009, la série GLONASS-K de satellites doivent être lancés. Ceux-ci devraient avoir une durée de vie de 10-12 ans et de transmettre trois signaux civils. En 2009/2010 les nécessaires 24 satellites devraient être en orbite (Figure 6339).

Figure 63: plan de développement de GLONASS

La précision de la position mesurée de GLONASS devrait progressivement se rapprocher de celle du GPS (Figure 64, [40]).

39 Sergey Revnivykh, Munich Sommet de navigation par satellite, 21-23 Février, 2006
40 Sergey V. Averin, européenne Conférence de navigation

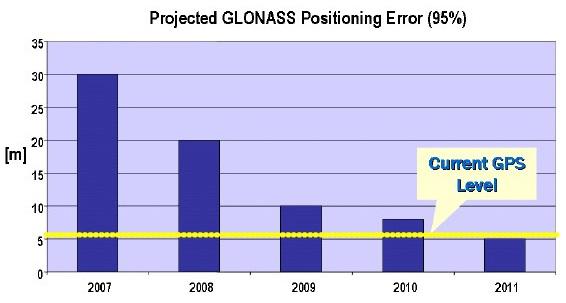
Figure 64: A la fin du développement de la précision de positionnement mesuré doit être égale à celle du GPS

Avec la modernisation et le déploiement de GLONASS les modifications suivantes au système peuvent être attendus:
· Renouvellement du segment de contrôle.
· Modernisation du principe du temps-référencement.
· Une mesure plus précise et la transmission des éphémérides et des temps de satellite.
· Amélioration de la stabilité des horloges des satellites.
· L'ellipsoïde de référence en cours d'utilisation (cadre de référence géodésique de PZ-90) sera approchée à ITRF.
· Un troisième signal civil (L3) sera introduit avec les satellites GLONASS-K.
· Une recherche et de sauvetage Fonction sera introduit avec GLONASS-K.
· Il est considéré également envoyer des signaux CDMA sur L1 plus tard GPS-

 

6 Calcule de la position

Si vous souhaitez . . .
o comprendre comment les coordonnées et le temps sont déterminées
o savoir ce que pseudorange est
o comprendre pourquoi un récepteur GNSS doit produire une estimation de position au début d'un calcul
o comprendre comment une équation non linéaire est résolu à l'aide de quatre variables inconnues
o sais ce degré de précision est affirmé par l'opérateur du système GPS
puis ce chapitre est pour vous!

6.1 introduction

systèmes GNSS combinent satellite sophistiqué et la technologie radio pour fournir des récepteurs de navigation avec les signaux radio indiquant entre autres le temps de transmission et l'identité du satellite émetteur. Le calcul de la position à partir de ces signaux nécessite des opérations mathématiques qui seront examinées dans le présent chapitre.

6.2 Calcul de position

6.2.1 Le principe de la mesure du temps de Voyage de signal (évaluation de pseudorange)

Pour un récepteur GNSS pour déterminer sa position, il doit recevoir des signaux de temps de quatre satellites séparés (Sat 1 ... Sam 4), afin de t4 (figure 74

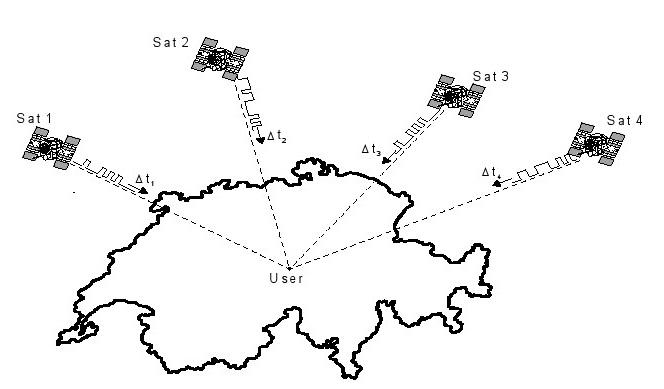
Figure 74: Quatre signaux satellites doivent être reçu

Les calculs sont effectués dans un système cartésien tridimensionnel de coordonnées ayant une origine géocentrique (figure 75). La portée de l'utilisateur à partir de chacun des quatre satellites R1, t1,DR2, R3 et R4 peut être déterminée à l'aide de voyage signal fois  t4 entre les quatre satellites et l'utilisateur.Dt3 et Dt2, D Étant donné que les emplacements XSAT, et YSat ZSat des quatre satellites sont connus, les coordonnées de l'utilisateur peuvent être calculées.

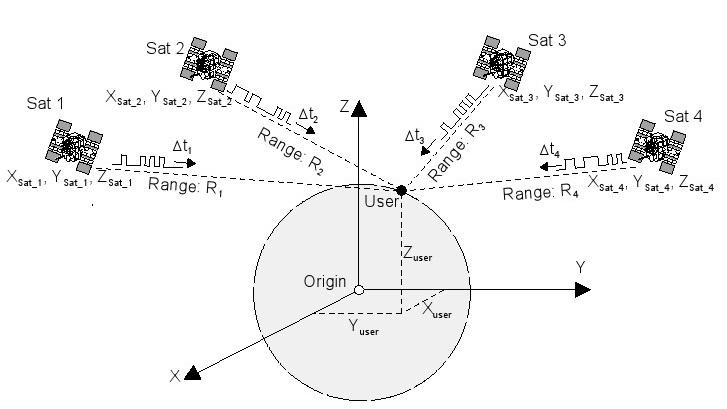
Figure 75: en trois dimensions le système de coordonnées

En raison des horloges atomiques à bord des satellites, le temps auquel le signal est transmis par satellite est connu de façon très précise. Toutes les horloges des satellites sont ajustées ou synchronisés entre eux et UTC (temps universel coordonné). t0.DEn revanche, l'horloge du récepteur ne soit pas synchronisé avec l'UTC et est donc lent ou rapide par  t0 est positif lorsque l'horloge utilisateur est rapide.DLe signe  t0 provoque des inexactitudes dans laDL'erreur de temps résultante  mesure du temps de Voyage de signal et la distance R. En conséquence, une distance incorrecte est mesurée que l'on sait que la distance de pseudo ou pseudo-PSR55.

 R: true range du satellite de l'utilisateur
c: vitesse de la lumière
t: Signal temps de Voyage à partir du satellite à l'utilisateurD
t0: différence entre l'horloge du satellite et l'horloge de l'utilisateurD
PSR: pseudorange
55 Manfred Bauer: Vermessung und Ortung mit Satelliten, Wichman-Verlag, Heidelberg, 1997, ISBN 3-87907-309-0

 

La distance R entre le satellite et l'utilisateur peut être calculée dans un système cartésien comme suit:

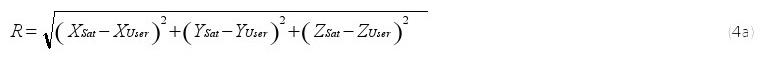
par conséquent (4) dans (3)

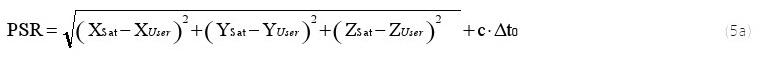
t0, xuser, YUser et Zuser), quatre équations indépendantes sont nécessaires.DAfin de déterminer les quatre variables inconnues

Ce qui suit est valable pour les quatre satellites (i = 1 ... 4):

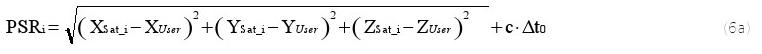
6.2.2 Linéarisation de l'équation
Les quatre équations 6a produisent un ensemble non-linéaire des équations. Afin de résoudre l'ensemble, la fonction racine est d'abord linéarisé selon le modèle Taylor, la première partie seulement utilisé (Figure 76).

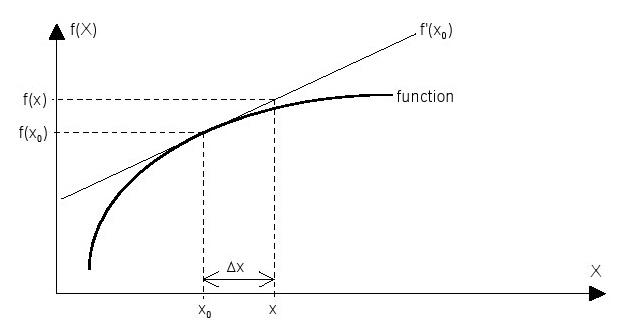
Figure 76: Conversion de la série Taylor

Afin de linéariser les quatre équations (6a), une valeur estimée x0 arbitrairement doit donc être incorporé dans le voisinage de x. Cela signifie qu'au lieu de calculer xuser, YUser et Zuser directement, une XTotal de position estimée, YTotal et ZTotal est d'abord utilisé (Figure 77).

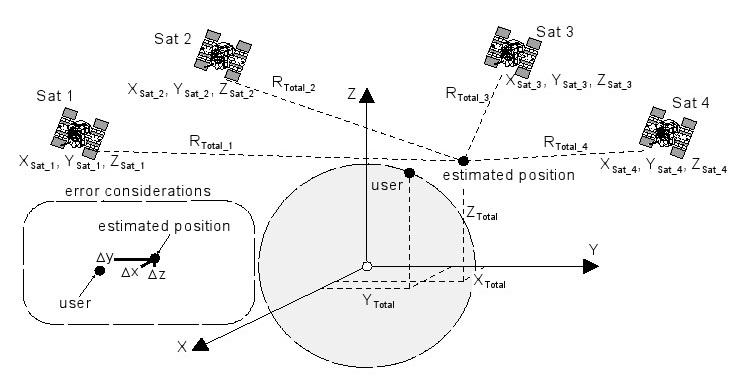
Figure 77: Estimation de position

z.Dy et Dx, DLa position estimée comprend une erreur produite par les variables inconnues

La distance Rtotal des quatre satellites sur la position estimée peut être calculée d'une manière similaire à l'équation (4 bis):

L'équation (9a) associé à des équations (6a) et (7a) produit:

Après avoir effectué une différenciation partielle, ce qui donne ce qui suit:

 

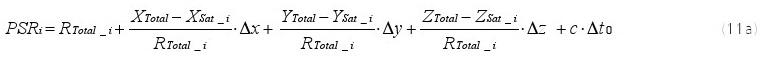
6.2.3 Résoudre l'équation
Après la transposition des quatre équations (11a) (i = 1 ... 4) les t0) peuvent maintenant être résolusDz et Dy, Dx, Dquatre variables ( selon les règles de l'algèbre linéaire:

z est utilisé pour recalculer la positionDy Dx, et DLa solution de  estimée XTotal, et YTotal ZTotal conformément à l'équation (8a).

Les valeurs estimées XTotal_New, YTotal_New et ZTotal_New peuvent maintenant être entrés dans l'ensemble d'équations (13a) en utilisant le x,Dprocessus itératif normal, jusqu'à ce que les composants d'erreur  z sont plus petits que l'erreur souhaitée (par exemple 0,1 m).Dy et D En fonction de l'estimation initiale de trois à cinq calculs itératifs sont généralement nécessaires pour produire une composante d'erreur inférieure à 1 cm.

6.2.4 Résumé
Afin de déterminer une position, l'utilisateur (ou le logiciel du récepteur de l'utilisateur) sera soit utiliser la dernière valeur de mesure, ou x,Dd'estimer une nouvelle position et calculer les composants d'erreur ( z) vers le bas à zéro par itération répétée.Dy et D Cela donne alors:

t0 correspond au récepteur erreur de temps et peut être utilisé pour régler l'horloge du récepteur.DLa valeur calculée de 

6.3 Détermination du temps de Voyage en détail

6.3.1 systèmes de temps

Pour déterminer les temps de trajet du signal à partir de satellites aux récepteurs, systèmes de temps différents sont importants (voir la section 3.5).
· UTC, temps universel coordonné (voir la section 3.5.2)
· Le temps GPS, le système de temps pour le système GPS. l'heure du GPS varie de UTC par un nombre entier de secondes (pour l'année 2008, la différence était de 14 secondes), plus une fraction de seconde à moins de 1μs. La différence entre le temps de GPS et l'UTC et les caractéristiques actuelles de cette différence sont communiquées dans le message de navigation (de Chassis 4, Page 18).
· Temps satellite, le temps de bord pour chacun des satellites individuels. La différence spécifique entre le temps par satellite et le temps GPS et les caractéristiques actuelles de cette différence sont également communiquées dans le message de navigation (de Chassis 1, Page 1-25).
· Récepteur Temps, le temps dans le récepteur GPS. Ce temps est généralement déterminé à partir d'un oscillateur à quartz interne et est différent du temps et / ou UTC GPS. La T0 différence est inconnue au début de l'exploitation d'un récepteur GPS, mais peut être réduit après quelques mesures.

6.3.2 Détermination du temps de Voyage en détail

La section suivante présente l'approche requise pour déterminer le temps de Voyage de signal. Afin de maintenir une vue d'ensemble de l'approche, la description de la procédure est grandement simplifiée. temps de Voyage est utilisé pour calculer la distance ou de la plage (R) entre le satellite et le récepteur. Figure 78 représente la dépendance linéaire de la plage (R) au temps de déplacement (indiqués sont les deux premières microsecondes).

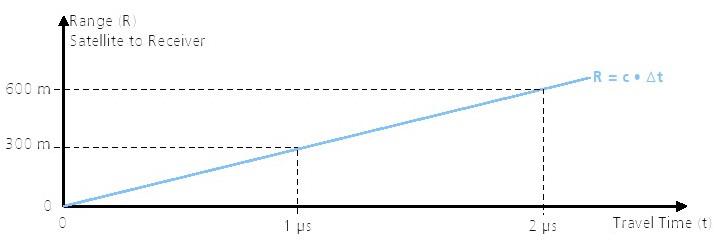
Figure 78: Détermination de l'intervalle (R) sur la base du temps de Voyage de signal

6.3.2.1 Phase 1: Détermination du temps d'arrivée de signal en utilisant la corrélation

Le récepteur GPS reçoit les signaux d'un ou plusieurs satellites. Pour chaque signal de corrélation a lieu. La procédure de corrélation décrite ici est un signal unique, mais il doit être fait pour chaque signal satellite.
Etant donné que le nombre (x) du satellite émetteur est pas connu du récepteur au moment de la réception du signal, il génère différents codes PRN (x = 1 ... 32). Ces codes sont décalés par rapport au temps jusqu'à ce qu'un PRN du code coïncide avec un maximum de corrélation pour le temps et la forme de signal pour le signal satellite x (figure 79: de corrélation maximale obtenue en décalant l'instant t2).

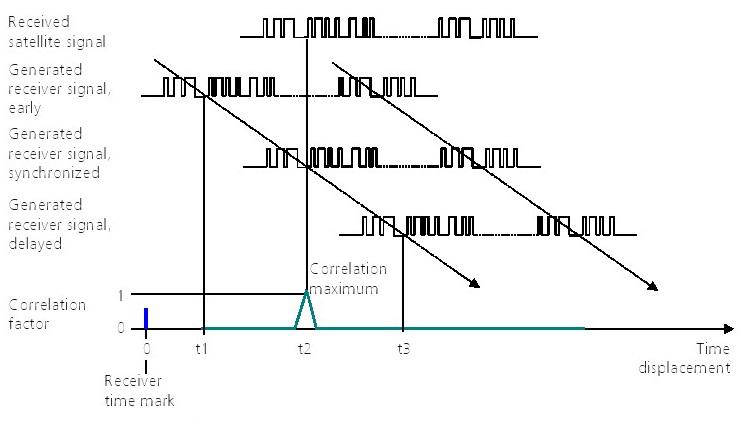
Figure 79: Corrélation en recherchant les maxima

Le tKo et la marque de temps du récepteurDdécalage de temps nécessaire  (intervalles de millisecondes par exemple) déterminer l'heure d'arrivée des signaux satellites observés (temps donné Récepteur Time). Dans la figure 80 l'heure d'arrivée mesurée revient à exactement 25min 2h 35,7293 ".

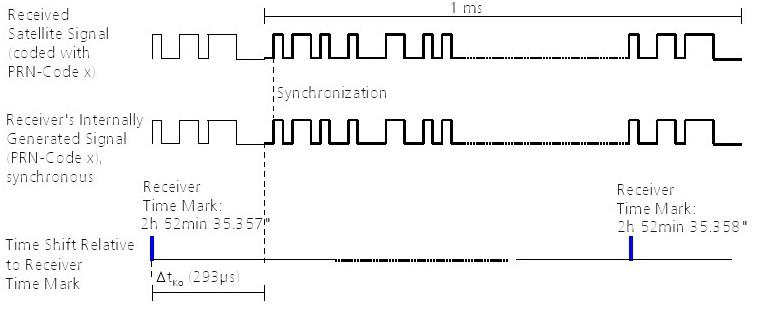
Figure 80: Détermination de l'heure d'arrivée du signal de satellite

 

6.3.2.2 Phase 2: la reconstruction des données et / ou messages de navigation
Le maximum de corrélation est séquentiellement recherchée et maintenue, à savoir, le signal satellite et de la PRN-séquence générée par le récepteur sont continuellement synchrone. La séquence PRN décalée dans le temps (/ A-code C) est lié au signal de satellite, et donc les données du message de navigation est reconstruit (voir Figure 81).

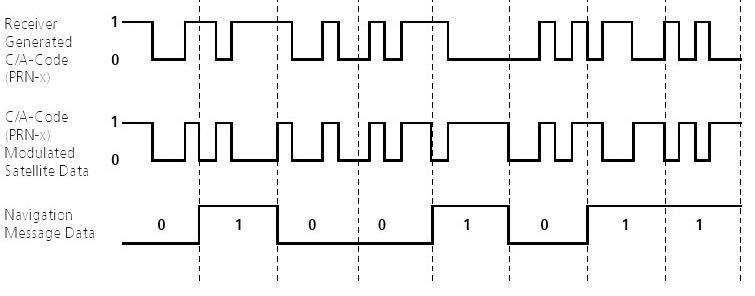
Figure 81: Reconstruction du message de navigation

6.3.2.3 Phase 3: Détermination du temps de transmission

Chaque sous-trame du message de navigation (voir également la section 4.6) commence par un préambule de 8 bits. Le préambule de la Telemetry Word (SLT) est un motif défini avec la structure 10001011. Cette séquence de bits est répétée toutes les 6 secondes. Le temps de transmission (en temps satellite) du préambule est inclus dans le Handover Word (COMMENT) de la sous-trame précédente avec le temps de 17 bits de la semaine (TOW) Message dans le message de navigation.

 

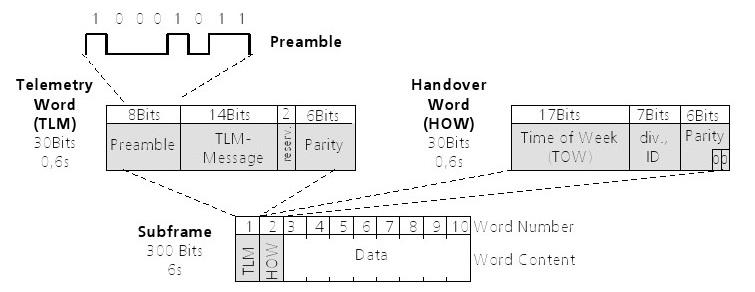
Figure 82: Telemetry Word (SLT) et Handover Word (COMMENT) du message de navigation

Le récepteur GPS cherche maintenant le Message de navigation pour le motif 10.001.011. Étant donné que ce modèle peut potentiellement apparaître dans d'autres parties du message de navigation, les conditions pour d'autres paramètres doivent également être respectées telles que:
· Deux 0s logiques doivent apparaître 51 et 52 bits après la fin du préambule pris (les deux derniers bits de parité dans le COMMENT sont mis à 0).
· La parité commençant 16 bits après le préambule supposé (parité du TLM Word) doit être correcte.
· Les deux bits avant le préambule pris doivent être 0 (les derniers bits de parité de chaque mot à la fin d'une sous-trame sont mis à 0).
· Le temps donné dans le message de TOW (17 bits) en commençant 22 bits après la fin du préambule doit être pris à peu près correcte. Puisque l'information de temps est à plusieurs reprises fourni toutes les 6 secondes, il n'y a aucune exigence de précision grands pour la mesure du temps récepteur.

• · Le préambule de la sous-trame suivante doit commencer exactement 300 bits suivant le début du préambule assumé.

Si le système permet d'obtenir une confirmation, puis tous les contrôles ne doivent être effectuées.
Le temps de transmission dans les premiers bits du préambule sont fournies dans le message de navigation dans le message TOW de la trame précédente. Ce temps est donné dans le temps par satellite, mais grâce à l'information dans le message de navigation, il peut être traduit en temps GPS.

6.3.3 Détermination de Voyage erreur de temps
Si le préambule est validé, l'heure d'arrivée des premiers bits dans le préambule est mesurée (voir 6.3.2.1). Cette fois-ci est donnée dans Receiver Time. Depuis Récepteur horaire et GPS ne sont pas identiques, mais diffèrent d'une t0, un temps de Voyage incorrecte est mesurée.Dvaleur de  Figure 83 illustre la procédure de détermination de l'erreur de temps de Voyage (cf Figure 78). Les deux échelles de temps différentes sont utilisées:
· Le temps GPS pour le temps de transmission du signal
· Récepteur Temps pour l'heure d'arrivée du signal.

 

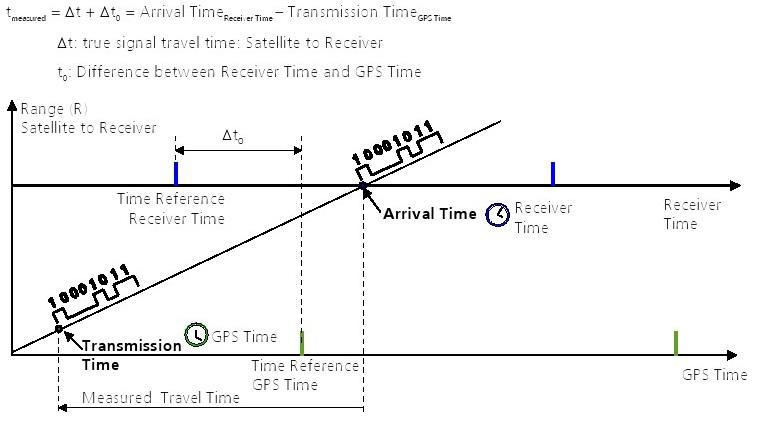
Figure 83: Détermination de Voyage erreur de temps

6.3.4 influences supplémentaires affectant le temps de Voyage
Le temps de Voyage de signal d'un satellite à un récepteur ne dépend pas seulement de la distance, mais est également influencée par un certain nombre d'autres facteurs physiques. Dans le document "Navstar GPS Espace Segment / Navigation utilisateur Interfaces56" exemples de l'utilisation de corrections prenant de nombreux paramètres en compte est présenté (Figure 84).

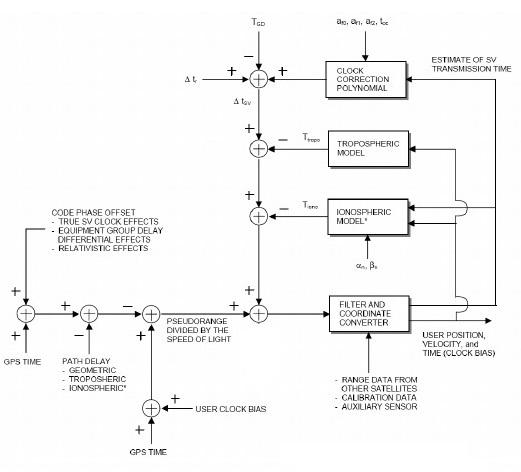
Figure 84 : Exemple de correction et de détermination du temps de transfert.

7 Le GPS : une précision toute relativiste

1 Structure du poster

Le plan est de commencer par expliquer le principe du dispositif général, en insistant sur la nécessité de maintenir tout le système parfaitement synchronisé. En effet, l’application du GPS peut-être la plus connue du grand public est le guidage des conducteurs de véhicules.

Cela nécessite que la position du véhicule puisse être estimée avec une précision de quelques mètres. Or les mesures de distances effectuées par le système sont basées sur des mesures de durée de propagation d’un signal électromagnétique, lequel voyage dans le vide à la vitesse c = 299 792 458 m/s.

Pour avoir la précision en position voulue, il est nécessaire que tout le système soit synchronisé à quelques nanosecondes près. Cet exigence est résolue grâce à plusieurs technologies : horloges atomiques à haute performance dans les satellites, surveillance permanente de ceux-ci, synchronisation permanente de l’horloge à quartz des récepteurs avec les horloges des satellites. Toute cette introduction occupe la première moitié du poster.

La seconde moitié du poster est destinée à vanter les mérites de la recherche fondamentale, même si cette dernière paraît déconnectée des applications immédiates. Je souhaitais expliquer que sans les travaux de Riemann sur la notion de variété abstraite au milieu du XIX e siècle, Einstein n’aurait pas pu concevoir sa théorie de la relativité générale (voir le poster de Marc et Jürgen). Or celle-ci prédit des effets qui compliquent la synchronisation du système : le potentiel gravitationnel de la Terre d’une part, et le fait que les satellites et les récepteurs soient en mouvement par rapport au référentiel inertiel géocentrique (c’est à-dire le référentiel galiléen d’origine le centre de la Terre et dont les axes de coordonnées pointent vers trois étoiles fixes) d’autre part, font que toutes les horloges du système GPS ne battent pas au même rythme. Ce phénomène n’est pas du tout anecdotique : le tableau à la fin du poster montre même que les dérives provenant de ces effets relativistes seraient la source principale d’erreur si elles n’avaient pas été prises en compte lors de la conception du système, loin devant le bruit des mesures ou les imprécisions sur la mesure de distance dues aux retards de propagation du signal lors de la traversée de l’atmosphère.

2 Anecdotes

Le nom officiel du GPS (Global Positioning System) est NAVSTAR (NAVigation System by Timing And Ranging). Il a été conçu et est géré par le Department of Defense (DoD) des Etats-Unis. Le DoD peut restreindre l’utilisation du système à tout moment, grâce à deux systèmes de protection. Le premier système, l’AntiSpoofing (AS), consiste à ne rendre possible la synchronisation précise du récepteur avec les satellites qu’aux utilisateurs autorisés ; en fait, les signaux rapides permettant cette synchronisation précise (le code P, voir plus loin) sont cryptés. Le second système de protection, la Selected Availability (SA), fait que les satellites transmettent des paramètres d’horloge et de position dégradés ; la dégradation est déterministe mais l’algorithme permettant la restitution des valeurs non dégradées est classifié militairement. La SA fait que le positionnement des utilisateurs non autorisés devient beaucoup moins précis (100 m). L’AS est activé en permanence, la SA a été désactivée en mai 2000 sur recommandation du président Clinton et ordre du Congrès américain.

La première génération de satellites GPS (bloc I), lancée entre 1978 et 1985, avait pour rôle de tester la faisabilité du système. Plus aucun satellite du bloc I n’est opérationnel.

Ce sont les satellites de la seconde génération (bloc II), lancés à partir de 1989, qui nous guident actuellement (le système a été déclaré opérationnel en 1995). Ces satellites sont équipés de plusieurs horloges atomiques, peuvent utiliser les systèmes AS et SA, et ont une durée de vie de l’ordre de dix ans. Les derniers modèles ont des fonctions de communication directe entre satellites GPS, permettant de pallier une éventuelle destruction de stations au sol (tout est prévu...)

Le système GPS comporte 24 satellites en activité, plus quelques uns en réserve. Leurs orbites sont quasiment circulaires (la plus forte excentricité est 0,01486). Les satellites sont répartis sur six plans orbitaux inclinés de 55◦ sur l’équateur ; la période est d’environ 12h.

En principe, un récepteur a besoin de recevoir les signaux de quatre satellites pour établir sa position et caler son horloge. En pratique, un récepteur capte davantage de satellites (jusqu’à douze) et se sert des signaux redondants pour améliorer sa position via une méthode des moindres carrés (encore des mathématiques...)

Certains responsables doutaient, au début du programme GPS, de la nécessité de tenir compte des effets de la relativité générale. Ainsi durant l’étude de faisabilité, il était possible de brancher ou de débrancher le système de compensation des effets relativistes sur un des premiers satellites GPS (NTS-2, lancé le 23 juin 1977). Après vingt jours de mesure, il fut décidé de laisser le système branché en permanence. De fait, là où la relativité générale prévoyait une dérive de 4, 465 10−10, la mesure donna 4, 425 10−10. L’effet relativiste est donc largement mesurable et maitrisable. L’erreur résiduelle de 1% s’explique par des dérives d’horloges, des imprécisions sur l’orbite, etc.

3 Signaux transmis par les satellites

Le débit d’information du signal émis par un satellite GPS est très lent : 50 bits/s. Ce signal contient :

– l’identification du satellite émetteur ;

– l’heure selon l’horloge du satellite ;

– les coefficients d’un polynôme quadratique donnant l’écart entre l’horloge du satellite et le temps atomique international ;

– les éphémérides de tous les satellites de la constellation (éléments képlériens de l’orbite et leur dérivée première par rapport au temps) ;

– des coefficients d’un modèle ionosphérique global simplifiée permettant d’estimer le retard pris par le signal GPS lors de la traversée de l’ionosphère ;

– des informations sur l’état de santé du satellite.

Ce signal est ensuite multiplié (multiplication dans le groupe {±1}) à un code dit «pseudo-aléatoire », qui est en fait périodique. Il y a en fait deux codes pseudo-aléatoires, le code C/A (Coarse/Acquisition, de fréquence 1,023 Mbits/s et de période 1 ms), ouvert à tous les utilisateurs et le code P (Precision, de fréquence 10,23 Mbits/s et de période 267 jours), classifié militairement. C’est en se synchronisant sur l’un ou l’autre de ces codes que les récepteurs peuvent établir le temps de réception du signal satellite (le code C/A est facilement repérable car lui ou son complémentaire est répété vingt fois dans chaque bit de données GPS transmis). Le signal P, dix fois plus rapide, offre une précision dix fois meilleure (bruit de mesure dix fois plus faible).

Le signal GPS ainsi encodé est alors émis en modulation de phase, sur deux fréquences (L1=1575,42 MHz et L2=1227,60 MHz). En comparant les temps d’arrivée du même signal sur les deux fréquences, un récepteur bifréquence peut estimer finement l’effet de l’ionosphère et le compenser en temps réel. Les récepteurs usuels ne sont que monofréquences (le code C/A n’est envoyé que sur la porteuse L1) et doivent donc se reposer sur le modèle simplifié transmis dans le signal des satellites pour estimer l’effet de l’ionosphère : c’est moins précis et le modèle n’est réactualisé qu’une fois par jour.

Les satellites ont une vitesse de quelques km/s par rapport aux récepteurs. Les signaux qu’ils émettent sont donc soumis à un effet Doppler, qui pourrait rendre ambigü la détermination de l’instant précis où le signal à moduler change. Les concepteurs du système ont ici trouvé une astuce géniale : la porteuse est une onde électromagnétique polarisée circulairement.

Quand le signal à moduler change de +1 à −1, la phase de la porteuse change de 180◦, et alors toutes les composantes du tenseur champ électromagnétique s’annulent.

La transformation de Lorentz préserve cette annulation du tenseur, ce qui garantit que le récepteur et l’émetteur voient bien le même événement, même s’ils sont relativement en mouvement.

Certains récepteurs sont capables de se synchroniser non pas sur les codes pseudoaléatoires, mais sur la porteuse elle-même, atteignant ainsi une précision millimétrique.

Cette possibilité, très délicate à mettre en oeuvre, n’est utilisée que pour effectuer des positionnements relatifs entre deux récepteurs — c’est fréquemment le cas en géodésie.

Dans ce cas, la plupart des sources d’erreur (connaissance imprécise de l’orbite des satellites, fluctuations de leurs horloges internes, délais de propagation du signal lors de la traversée de l’atmosphère...) sont quasiment les mêmes pour les deux récepteurs et s’éliminent donc dans le résultat final.

4 Effets relativistes

Un excellent article de survol est disponible sur le Web : Relativity in the Global Positioning System, par Neil Ashby, Living Rev. Relativity 6, (2003),

http://www.livingreviews.org/lrr-2003-1

.

Les spécifications officielles du système GPS prévoient la prise en compte de cinq effets relativistes :

– l’effet de la masse de la Terre sur le décalage gravitationnel en fréquence des horloges atomiques de référence fixées à la surface de la Terre par rapport à des horloges à l’infini ;

– l’effet de la distribution de masse non sphérique de la Terre pour le décalage gravitationnel en fréquence des horloges atomiques fixées à la surface de la Terre ;

– le décalage Doppler du second ordre sur les horloges fixées à la surface de la Terre dû à la rotation de la Terre ;

– le décalage gravitationnel en fréquence des horloges des satellites GPS dû à la masse de la Terre ;

– le décalage Doppler du second ordre sur les satellites GPS dû à leur mouvement dans un référentiel inertiel géocentrique.

Les lignes qui suivent ont vocation à expliquer ce charabia. Les trois premiers points concernent l’établissement du temps de référence disponible sur toute la surface de la Terre.

Reprenons la formule du poster pour le ds2 :

 

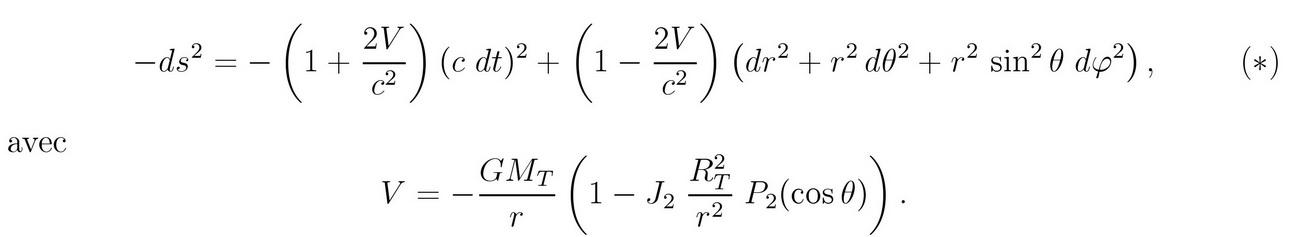
Ici t (temps mesuré par une horloge idéale placée à l’infini, au repos et hors de tout champ de pesanteur), r (distance au centre), µ (colatitude), et ' (longitude) sont des coordonnées dans un référentiel inertiel géocentrique (c’est-à-dire un référentiel galiléen d’origine le centre de la Terre et dont les axes de coordonnées pointent vers trois étoiles fixes). Pour passer à un référentiel lié à la Terre (tournant avec elle), il faut faire la substitution

' =

'

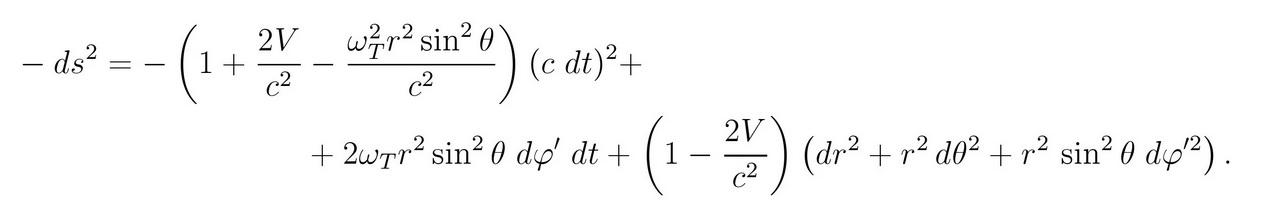
′ + !T t, où '′ est la longitude mesurée à partir du méridien de Greenwich et !T =

7, 2921151467 10−5 rad/s est la vitesse de rotation de la Terre sur elle-même. On arrive alors à

 

Notons

© = V − (!2Tr2 sin2 µ)/2  le potentiel gravitationnel effectif, incluant un terme potentiel dû à la force centripète. La racine carrée du coefficient

g00 = −(1 + 2©/c2) de la métrique pseudo-riemannienne est alors égale au rapport entre le temps coordonnée t et la fréquence propre d’une horloge atomique fixe dans le référentiel lié à la Terre et placée dans le champ de pesanteur de cette dernière. Le géoïde de référence est la surface équipotentielle © = © 0, où ©0/c2 est conventionnellement fixé à 6, 969290134 10−10. Ce géoïde est en gros un ellipsoïde aplati représentant la surface de notre planète au niveau moyen des mers.

Sur ce géoïde de référence, toutes les horloges atomiques battent au même rythme : quand on s’approche du pôle, le potentiel newtonien augmente, causant un ralentissement de l’horloge, mais cet effet est exactement compensé par un effet Doppler du second ordre (appelé « dilatation des temps » dans la littérature traitant de la relativité restreinte) dû au fait que la vitesse par rapport au référentiel inertiel diminue. Il est alors possible de définir une échelle de temps qui soit donnée par des horloges idéales fixées au géoïde.

Cet échelle, réalisée physiquement par un réseau mondial d’horloges atomiques, est appelé temps UTC (temps universel coordonné).

C’est avec cette échelle de temps (plus exactement, sur sa réalisation par l’US Naval Observatory) que les satellites GPS sont synchronisés. C’est un choix heureux, car nos récepteurs GPS indiquent alors ce temps UTC lorsqu’ils se calent lors d’une mesure de position.

Les deux derniers des cinq effets de la relativité générale prise en compte dans les spécifications du système GPS concernent les satellites. On part à nouveau de ( ¤). Le potentiel V provoque un ralentissement des horloges embarquées par rapport au temps t des horloges à l’infini, mais ce ralentissement est moindre que celui des horloges au sol. Ainsi les horloges embarquées battent plus vite que les horloges au sol. De plus, les satellites sont aussi en mouvement, d’où un effet Doppler du second ordre. (Pour calculer précisément ce dernier, il faut substituer les équations du mouvement du satellite dans (¤).) Ce sont ces deux facteurs qui engendrent la dérive entre horloges au sol et horloges embarquées de 38,5 μs/jour mentionnée sur le poster. Les satellites sont programmés « en usine » pour modifier la fréquence de leur horloge atomique et compenser cet effet, qui reste donc caché à l’utilisateur final.

Enfin, les orbites des satellites ne sont pas parfaitement circulaires. Les variations d’altitude du satellite entraînent une variation du potentiel gravitationnel et une variation de leurs vitesses (les deux variations sont liées par le principe de conservation de l’énergie et par le théorème du viriel), d’où à nouveau deux termes correctifs à ajouter pour le calcul de l’influence sur les fréquences d’horloge. Pour le satellite le plus excentré, l’écart en temps maximal est de l’ordre de 23 ns. Les récepteurs GPS sont programmés pour tenir compte de

cet effet, qui est calculable puisque le récepteur dispose des paramètres de l’orbite de tous les satellites. (Les satellites GPS pourraient effectuer la correction eux-mêmes et modifier le signal qu’ils émettent en conséquence. Ils ne le font pas, au contraire des satellites du système concurrent russe, le GLONASS.)

Signalons pour finir que le terme quadrupolaire dans le potentiel gravitationnel terrestre V  causé par l’aplatissement de notre planète, contribue à faire que les orbites des satellites ne sont pas circulaires. De fait, il cause une variation d’altitude de l’ordre de quelques centaines de mètres.

L’effet de cette variation sur la fréquence d’horloge des satellites est très faible (beaucoup plus que tous les autres effets mentionnés ici), mais le fait en lui-même est amusant et méconnu.

5 Traversée de l’atmosphère

L’atmosphère est modélisée en plusieurs couches, tel un onion. Entre 0 et 10 km se trouve la troposphère ; c’est là où se trouve l’humidité et les nuages. Entre 10 et 50 km, il y a la stratosphère : la couche d’ozone ou ce qu’il en reste y est localisée. Puis la mésosphère, entre 50 et 80 km, consume les étoiles filantes. Entre 80 et 500 km est la thermosphère, qui abrite notamment l’ionosphère, une zone où les molécules sont ionisées et où il y a donc des électrons libres qui perturbent le signal électromagnétique. Au delà, il y a l’exosphère.

En présence de matière, la vitesse d’un signal électromagnétique est inférieure à c. Il faut tenir compte de cela quand on estime la distance entre un récepteur et les satellites à partir de la durée de propagation du signal. Les couches atmosphérique incriminées sont l’ionosphère (sa traversée cause un retard de quelques dizaines de nanosecondes pour un satellite au zénith) et la troposphère (retard de l’ordre de 10 ns). La valeur (1 ou 10 ns) indiquée sur le poster est assez fantaisiste, je ne sais plus d’où je l’ai tirée... L’estimation précise de ces retards est assez délicate, surtout pour la troposphère. L’erreur induite sur le positionnement horizontal du récepteur est cependant limitée, les signaux de tous les satellites étant affectés (le retard est en fait d’autant plus grand que le satellite est bas sur l’horizon).

Du fait de la présence d’électrons libres, la troposphère est un milieu dispersif : la vitesse de groupe, à laquelle se propagent les signaux C/A et P, varie selon la fréquence. Le retard de propagation du signal est donc différent pour la fréquence L1 et la fréquence L2. Les récepteurs bi-fréquence peuvent alors faire une estimation précise de la densité d’électrons libres dans l’ionosphère et compenser cet effet. Les récepteurs habituels (monofréquence L1) se reposent quand à eux sur le modèle simplifié de l’ionosphère transmis dans le signal délivré par les satellites. A noter enfin que le système GPS est fortement perturbé dans les régions subissant des aurores boréales.

Les retards que cause la traversée de la troposphère sont difficiles à estimer, car ils dépendent des conditions météorologiques (température, présence de nuages ou d’humidité dans l’air, etc.) C’est actuellement la première cause d’imprécision du système GPS pour la détermination de la hauteur. Inversement, la mesure de cet effet à des stations de position connue avec précision fournit des données sur l’état de la troposphère qui peuvent ensuite être prises en compte dans les modèles météorologiques ou climatiques.

6 Galileo

Galileo est le futur système européen de positionnement par satellites. Son mode de financement public et privé est à l’origine d’un gros retard dans le programme. Là où le GPS américain est d’utilisation essentiellement gratuite (on paie certes le fabriquant du récepteur et l’éditeur du logiciel et des cartes, mais on ne paie pas pour l’accès aux signaux des satellites), le système européen devrait être en partie payant. Contrairement à ce que disent nos médias, beaucoup d’états ou d’entreprises européens sont prêts à payer, mais peu acceptent de partager le contrôle du système. En attendant que nous résolvions nos querelles intestines, le parc de récepteurs du système américain augmente très rapidement...

Signalons pour conclure que les Russes, les Japonais et les Chinois commencent également à mettre en place leur système, le système japonais ne visant toutefois pas à une couverture mondiale.

7